Calculus II Online Course for Academic Credit
STEM Calculus II is the second course in the freshman (engineering) calculus sequence (STEM: Science, Technology, Engineering, and Mathematics), usually referred to as a course on "Integration Theory". With Calculus I concentrating mainly on the derivative and getting to the Fundamental Theorem of Calculus, Calculus II investigates integrals both how compute them algebraically (when you can), numerically (using numerical methods), and then using infinite polynomials (Power Series) to approximate integrals when you cannot compute them algebraically.
| Course Title: | STEM Calculus II |
| Catalog Number: | DMAT 263 |
| Credits: | 4 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for STEM Calculus II |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 263 - STEM Calculus II | |
Completion of DMAT 263 - STEM Calculus II earns 4 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
STEM Calculus II Introductory Videos
STEM Calculus II Course Introduction
The second semester of 1st year Calculus is the preparatory course for all of the 2nd year courses (Multivariable Calculus, Differential Equations, Linear Algebra). Often referred to as "the first course on integral calculus", Calculus II focuses on a more practical, computational command of the integral, which is only introduced as a concept in Calculus I.
STEM Calculus II is comprised of two distinct parts:
- Techniques of Integration
When you (or a computer) can algebraically integrate a function, how is that accomplished? Essentially, the Rules of Differentiation are "inverted" to the integral, providing the main strategies for attacking the algebraic integral - when possible. - When Algebraic Integration Just Can't Be Done
The vast majority of functions cannot be algebraically integrated - there just is no algebraic antiderivative for such functions. The development of "Plan B" for attacking these types of algebraic integrals comes in the form of expanding the way we describe functions, not just with the elementary class of functions including such friends as sin(x), ex, x1/2, etc. but with a more generalized description based upon infinite polynomials. This raises all kinds of questions that have to be studied, but once accomplished, we are able to conquer these algebraic integrals.
STEM Calculus 2 - The Longest Course
Calculus II is the longest course in the Calculus sequence.
Many students feel that Calculus II is the most difficult course in the Calculus sequence as well.
Our Calculus II course has the following components:
- Integral Calculus Refresher
Calculus II starts with an intensive 40 assignment refresher of introductory integral calculus, starting from the definition of the integral via signed area, ranging to beginning algebraic integration, the Fundamental Theorem of Calculus, and initial applications of the integral. As many students start in our Calculus II course, having studied Calculus I elsewhere, it is important for all students to have this common foundation moving forward into the Calculus II course. - Techniques of Integration
One of the goals of Calculus II is to become an expert in algebraic integration: finding antiderivatives. Computer algebra tools can find antiderivatives automagically, so an exploration of the techniques of antiderivatives must contain an meaningful mixture of integration concepts, manual skills, and usage of computer algebra software. Traditional Calculus II courses explore these techniques purely from the paper/pencil standpoint, which has merits and drawbacks in this modern age. We strive for a balance between classical and modern computational mathematics in a unique way. For example, a more advanced integration technique known as Integration via Differentiation is presented, which is absent from all traditional textbooks, since it is computationally difficult with only manual tools - it is the leverage of computer algebra tools that makes this technique come alive. - Double Integrals and Gauss-Green Theorem
Calculus II starts the dimensional generalization of integration theory, into double (or 2D) integrals, which can be used to measure volume and other applications. Double integrals initially come in two varieties: over 2D regions that are essentially rectangular, and over 2D regions that are not rectangular, but whose boundary curve can be formulated. In the latter case, the Gauss-Green Theorem is utilized; it is common for this theorem to be explored only in Multivariable Calculus, but we do this theorem early as an introduction to the higher dimensional Fundamental Theorem of Calculus. - When Algebraic Integration Cannot Be Completed
The second half of Calculus II explores the problem: What to do when you cannot find an antiderivative to a function, like f(x) = x * tan(x) ? The limitation is not a matter of cleverness - one can prove that this function has no algebraic integral in terms of elementary functions (exponential, log, trig, roots, finite polynomial, etc.) This leads to the concept of a function polynomial expansion - a way to approximate a function by polynomials (bridging to equality when considering infinite polynomials). Moving to this new way of describing functions beyond elementary functions allows integration to be accomplished. As a result of polynomial expansions, infinite sequences and series are studied - a flipped order as found in all traditional calculus textbooks. - Introduction to Vector Calculus
To meet transferability requirements, Calculus II has a few introductory lessons on 3D geometry: lines, planes, vectors, dot products, cross products.
Why is the Calculus II so long? Historically and nationally, it has always been so. Calculus II has the reputation of being the barrier course to 2nd year Calculus - colloquially, the "weed-em out course". One reason for so many topics is for articulation/transferability to the majority of colleges/universities in the U.S.
Roger Williams University Course Catalog Listing: DMAT 263 - STEM Calculus II
Course: DMAT 263
Course Title: STEM Calculus II
Transcript Course Title (30 Characters Max:): STEM Calculus II
Course Description: A second course in the differential and integral calculus for engineering and science with emphasis on computational techniques, graphical analysis, and algebraic methods. Topics include integration theory, algebraic methods of integration, integral functions and transformations, improper and numerical integrals, applications of integration to geometry and physics, double integrals, integration over regions with parametric boundary, splines, barriers, Taylor's Theorem, L'Hopital's Rule, infinite sequences and series. [4 Semester Credits]
Prerequisite: Successful completion (C- or higher) of Calculus I or equivalent, or consent of instructor.
E-Textbook: Calculus & LiveMath by Robert R. Curtis, Ph.D., adapted from Davis/Porta/Uhl Calculus&Mathematica courseware series
Software: LiveMath
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 263 - STEM Calculus II
DMAT 263 - STEM Calculus II - Learning Outcomes
- 1. To understand and compute algebraic integrals using a variety of symbolic techniques, including substitution, integration by parts, iteration methods
- 2. To understand and compute with the Fundamental Theorem of Calculus
- 3. To understand and compute solutions to applications problems involving integrals
- 4. To compute measurements of volumes of geometric objects using integrals (slides, surfaces of rotation
- 5. To understand and compute with Green's Theorem
- 6. To understand and compute parametric and Polar function integrals
- 7. To understand and compute double integrals
- 8. To understand and compute splines and polynomial approximations
- 9. To understand and compute with Taylor's Theorem
- 10. To understand and compute with L'Hopital's Rule and using expansions to compute limits
- 11. To understand and compute sequences and series
- 12. To understand and compute convergence or divergence of sequences and series
- 13. To understand and compute 3D vector analysis, dot product, planes, and cross products
DMAT 263 - STEM Calculus II - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. Integration 2.1 Measuring Area Under a Curve 2.2 Definition of the Integral 2.3 Properties of Integrals, Symmetry 2.4 Integrals of Data Functions 2.5 Numerical Methods: Rectangles, Trapezoids 2.6. Undefined Integrals 2.7 Numerical Calculation of Integrals 3. Fundamental Theorem of Calculus 3.1 Derivative of an Integral 3.2 Integral of a Derivative 3.3 Fundamental Formula 3.4 Distance, Velocity, and Acceleration 3.5 Improper Integrals 3.6 More Properties of Integrals 3.7 Applications: Measure Accumulation Totals 3.8 Indefinite Integrals and Antiderivatives 4. Measurements via Slicing 4.1 Measuring Area via Slicing 4.2 Measuring Volume via Slicing 4.3. Density and Mass 4.4 Accumulation of Rates 4.5. Arc Length 5. Computing Integrals 5.1 Algebraic Antiderivatives 5.2. Integrals of Standard Functions: Polynomial, Exponential, Trigonometric, Logarithmic 5.3 Transforming Integrals: u-substitution 5.4 Measuring Area under Parametric Curves 5.5 Integrals of Polar Functions 6. Measurements via Slicing 6.1 Measuring Area via Slicing 6.2 Measuring Volume via Slicing 6.3 Density and Mass 6.4 Accumulation and Rates 6.5 Arc Length 7. Double Integrals 7.1 Measuring Area and Volume 7.2 Gauss-Green Formula 7.3 Changing Order of Iterated Integrals 8. Integration Techniques 8.1. Separable Differential Equations 8.2 Integration By Parts 8.3 Integration Patterns and Reduction Formulas 8.4 Partial Fractions Technique 8.5 Trigonometric Integrals 8.6 Trigonometric Substitution 9. Taylor's Expansion of a Function 9.1 Splines and Smooth Splines 9.2 Points of Contact 9.3 Application: Landing an Airplane 9.4 Taylor Expansion 9.5 Recognizing Familiar Expansions 9.6 Using Expansions for Approximations 9.7 Derivatives and Integrals of Expansions 9.8 Expansions At Other Points 9.9 Newton's Method 9.10 Calculating Limits: L'Hopital's Rule 10. Sequences and Series 10.1 Sequences of Numbers 10.2 Series of Numbers 10.3 Convergence 10.4 Convergence of Taylor Expansions 10.5 Barriers: Radius of Convergence 10.6 Shared Convergence Intervals for Derivatives and Integrals of Functions 10.7 Applications: Drug Dosing 11. Power Series 11.1 Basic Definition 11.2 Convergence Intervals of Power Series 11.3 Ratio Test and Other Convergence Tests 11.4 Finding Series Convergence Values via Power and Taylor Series 12. Polar Coordinates 12.1 Basic Graphing 12.2 Recognizable Curves 12.3 Differentiation and Integration in Polar Coordinates 13. Vector Analysis 13.1 Vector Arithmetic 13.2 Dot Product, Cross Product 13.3 Planes 13.4 Partial Derivatives 13.5 Tangent Planes
Legacy Course Connection
Legacy Distance Calculus Course:
DMAT 214 - Calculus II with Lab
In 2023, Distance Calculus introduced a new catalog of courses. The connection between the old courses and the new courses are given here:
Legacy Course Description: Covers the integral calculus of algebraic and transcendental functions and its applications. Topics include elementary differential equations, computation of areas, volumes, work and other physical quantities, integration techniques, improper integrals, and infinite series. The laboratory component involves use of computer algebra software. (4 credits)
Calculus II Example Student Profiles
Case 1: Calculus I Done, Now Calculus II
For many students, planning for the Calculus II course is simply the natural progression from completing the Calculus I course, as part of their particular educational plan of study.Often students have the sights set on one of the second year courses:
- Multivariable Calculus
Usual course for majors in Economics, Physics, Engineering, Science - Differential Equations
An essential course for physics and engineering students - Linear Algebra
An essential course for physics, engineering, and computer science students. - Calculus-Based Probability
Required course for advanced economics, finance, bio-statistics, and other math-heavy graduate degrees.
| Typical Completion Timelines for DMAT 263 - Calculus II | ||||
| Hours Dedicated | Calculus I Grade | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-10 hours/week | C,D | 1-2 hours/day | 16 weeks | Reasonable |
| 7-12 hours/week | C,D | 2-3 hours/day | 14 weeks | Reasonable |
| 10-15 hours/week | C+,B,B+ | 3-4 hours/day | 10 weeks | Reasonable |
| 15-20 hours/week | B | 5-6 hours/day | 8 weeks | Stretched |
| 20-25 hours/week | A | 5-7 hours/day | 6 weeks | Stretched |
| 25-35 hours/week | A+ | 6-8 hours/day | 4 weeks | World's Record |
Case 2: Undergraduate Science Major
Rafael is a undergraduate chemistry major, and part of his degree program dictates that he finish Calculus I and II. Rafael did pretty well in Calculus I, but wants to try something different for Calculus II, and to take the course via Distance Calculus.How fast can Rafael complete the Calculus II course?
The answer to this question depends mostly on when Rafael plans to work on the course.
The most successful time for Rafael would be during winter, spring, or summer breaks from his regular course load. By modifying his schedule to work on the Calculus II course during these "off times", Rafael will be able to concentrate and focus just on the Calculus II course, and his tendency towards success will increase dramatically.
If Rafael must complete the Calculus II course during the regular semester, as part of the other 3-5 courses he is taking, trying to fit Calculus II in there will be challenging. Here are some timelines for such a plan:
| Calculus II Course Plan With Full Course Load Otherwise | ||||
| Hours Dedicated | Calculus I Grade | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 9 hours/week | C | 3 hours/day, 3 days/week | 18 weeks | Reasonable |
| 12 hours/week | C | 3 hours/day, 4 days/week | 14 weeks | Reasonable |
| 12 hours/week | B | 3 hours/day, 4 days/week | 12 weeks | Reasonable |
| 15 hours/week | B | 3 hours/day, 5 days/week | 10 weeks | Stretched |
| 15 hours/week | A | 3 hours/day, 5 days/week | 8 weeks | Stretched |
| 18 hours/week | A+ | 3 hours/day, 6 days/week | 6 weeks | Ambitious |
Case 3: Returning To Graduate School: Rushed
Kathy just got accepted into Graduate School in Economics towards a Ph.D. She has a conditional acceptance, and must finish Calculus II in a very short time. Kathy also works full time.What must Kathy do to finish Calculus II?
The "short time" needs to be on the order of 4-6 weeks for Calculus II. Anything less is quite impossible. Calculus II is just too long and difficult to complete in any less time. Kathy will also need to plan to be on the C grade path - which will lower her syllabus requirement by 30%. As the graduate school only needs demonstration that the Calculus II course was completed with a grade of C or above, and this grade will not transfer to Kathy's GPA, a C grade is planned for. (If Kathy finishes her C syllabus earlier than expected, she may go back and complete the additional assignments to move back to the B or A grade paths).
Kathy will need to plan for large blocks of time to dedicate towards the course. If shooting for 4 weeks completion, then at least 8-10 hours per day. If shooting for 6 weeks completion, then 6-8 hours per day, every day. It will be a very challenging 4-6 weeks.
Kathy should also be ready that the course takes a little longer than the planned 6 weeks. Going a week or two over to 8 weeks is quite common. Usually graduate schools are quite understanding of the situation of "I'm almost done", and in many cases, the graduate school will give a short extension to aid the student with harsh deadlines.
Kathy must understand that even though there are some tough deadlines with this plan, that does not mean that "corners are cut" in the Calculus II course because of these extenuating circumstances. There is only 1 way through the course, and that is the right way.
Case 4: Returning To Graduate School: Methodical
Halley is applying to Graduate School in Biostatistics towards a Ph.D., and will start in 1 year. Halley knows she must complete Calculus II prior to starting that course work (and even before submitting the graduate school application).What will the Calculus II course look like for Halley?
Halley is not in a rush, yet she wants to finish the course methodically, in a timely manner, as quickly as possible. As Halley is a Ph.D. bound student, she is highly motivation and task-completion oriented. Some timelines for Halley for Calculus II might look like this:
| Graduate-Bound Student Timelines for DMAT 263 - Calculus II | ||||
| Hours Dedicated | Calculus I Grade | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-7 hours/week | C | 1-2 hours/day | 18 weeks | Relaxed |
| 8-12 hours/week | B | 2-3 hours/day | 10 weeks | Reasonable |
| 10-14 hours/week | B+/A | 3-4 hours/day | 8 weeks | Reasonable |
| 14-20 hours/week | A | 4-5 hours/day | 6 weeks | Ambitious |
Time commitments are important for success in an online Calculus II course for college credit from Distance Calculus. There are no fixed due dates in the Distance Calculus online courses, so it is important that students instead set their schedules for a dedicated amount of time towards the coursework.
It is also very important to consider that going faster through a course is DIRECTLY DEPENDENT upon your math skill level, and your successful engagement of the course. We require that you complete the course in a Mastery Learning format. If you are struggling with the course content, or trying to go too fast where the quality of your submitted work is suffering, then the instructors will force a slow-down of your progress through the course, even if you have fixed deadlines.
The typical path for students like Halley is the 8-10 week plan.Case 5: Lack of Success in Classroom Calculus II Course
Al took Calculus I and did OK in the course, earning a C grade. Then Al went onto Calculus II, hoping to improve his grades, but found Calculus II to be considerably more difficult than Calculus I, and ended up earning a D grade (or not passing).Al loathes the thought of returning to the classroom lecture for Calculus II. The lectures were not that much fun going through them the first time, and trying to sit through them a second time will be more than just painful.
Al wants to change gears, and try something new - taking Calculus II via Distance Calculus.
Typically, students like Al will take the course over the summer months, and be able to focus just on the Calculus II course, without being overwhelmed by multiple courses all vying for Al's attention.
Al should plan to take a step back, a deep breath, and engage the course as if starting on a marathon race. Just because Al "had Calculus II already", this poor foundational knowledge will not help Al succeed in this second (and quite different attempt).
Al would be approaching Calculus II from a completely different viewpoint than his previous attempt, which certainly goes a long way to minimizing the "review" nature of repeating a course. When going through the new Calculus II course, all will see things he saw before (e.g. integrals), but completely different types of questions that he probably saw in the classroom/textbook course. An open mind, and genuine academic curiousity to investigate and embrace the new style of work will be required for success.
Al should plan for a minimum of 12 weeks to engage the course, even during the summer. It will take time for the course concepts and materials to "sink in" and become comfortable.
We have had many students like Al succeed in Calculus II where their classroom experience with Calculus II was a failure. However, we have also had many students like Al who discover that the reason they didn't succeed in their first attempt at Calculus II was an indicator that their math skills are not strong, their interest in math is weaker, and their chosen course study plan may need to change upon failure in two different course paradigms.
Case 6: AP Calculus BC Equivalency
Anwar is a hot-shot high school student. He has completed AP Calculus AB (equivalent to Calculus I), and instead of taking the AP Calculus BC exam, he wants to jump ahead and take the Calculus II course from Distance Calculus, earn collegiate credits directly, and transfer them to his planned university (that he currently has applications out to).Anwar will most likely be able to finish the Calculus II course very quickly with a dedicated effort that is quite natural for him. 6-8 weeks is the common time frame.
However, Anwar may discover that Calculus II via Distance Calculus is an adult course, and quite unlike the high school course paradigm that he has been so successful in previous. Some students like Anwar can find Calculus II more difficult than they anticipated, and they have to dedicate more time and effort than they had planned to budget for.
While Anwar can earn collegiate credits for Calculus II in a similar way that AP Calculus BC would earn, Anwar would not benefit from the inflated GPA multiplier that AP courses help with high school GPAs.
On the plus side, quite often schools (mostly graduate schools) will not accept AP Calculus course credit for satisfaction of program prerequisites. Some schools are starting to insist that higher courses - like Calculus II - be completed a real collegiate courses, and not "waived via AP Exam". We have seen more than a few students have to return to Distance Calculus to re-take Calculus II again as a real collegiate course, as they graduate program would not accept the AP Calculus BC exam completed in high school as proof of Calculus II completion.
Calculus II Distance Calculus Referenced Colleges/Universities
Over the past 27 years, Distance Calculus has enrolled thousands of students who successfully complete the Calculus I course, and use this course record towards undergraduate and graduate programs at various colleges and universities in the U.S. and throughout the world.Below is a list of schools (most recently, from just 2010-2013) that Distance Calculus - Calculus I students have listed as their Home Institution:
- Penn State University
- Purdue University
- Rensselaer Polytechnic Institute
- Rutgers University
- SUNY Binghamton
- Syracuse University
- Texas A&M University
- Texas Tech University
- The George Washington University
- The Ohio State Universtity
- The University of Texas at Austin
- The University of Virginia
- University of Georgia
- University of Arizona
- University of Arkansas, Little Rock
- University of California, Berkeley
- University of Chicago
- University of Cincinnati
- University of Colorado, Boulder
- University of Colorado,Colorado Springs
- University of Connecticut
- University of Maine
- University of Massachusetts, Amherst
- University of Minnesota
- University of New Hampshire Law School
- University of New Haven
- University of North Carolina at Chapel Hill
- University of North Texas
- University of Oklahoma
- University of Tampa
- University of Texas, Arlington
- University of Texas, Austin
- University of Texas, Brownsville
- University of Texas, Dallas
- University of Texas, Houston
- University of Virginia
- University of West Georgia
- University of Wisconsin, Madison
- University of Wyoming
- Boston University
- Arizona State University
- California Polytechnic State University, San Luis Obispo
- Clemson University
- Colorado State University
- Cornell University
- DePaul University
- Drexel University
- Georgia State University
- Iowa State University
- Johns Hopkins University
- Kansas State University
- Loyola Marymount University
- Miami University
- Michigan State University
- Michigan Technological University
- Missouri University of Science and Technology
- Montana State University
- Roger Williams Univerity
- Smith College
- Agnes Scott College
- Athens State University
- Baruch College
- Bentley University
- Berklee College of Music
- Binghamton University
- Bluefield State College
- Bluegrass Community and Technical College
- California Lutheran University
- California Polytechnic State University, San Luis Obispo
- California State University Channel Islands
- Cedarville University
- Chapman University
- Charter Oak State College
- Clark University
- CUNY Medgar Evers College
- Eastern Kentucky University
- Eastern Mennonite University
- Eastern Nazarene College
- Embry Riddle University
- Excelsior College
- Ferris State University
- Florida Institute of Technology
- Hamline University
- Hofstra University
- Illinois Institute of Technology
- Kennesaw State University
- Kettering University
- Lebanon Valley College
- Liberty University
- Lipscomb University
- Luther College
- Macon State College
- Marquette University
- Mars Hill College
- Marshall University
- Mercer University
- Messiah College
- Morehead State University
- North Carolina Agricultural and Technical State Univerisity
- Occidental College
- Saint Louis University
- Saint Michael's College
- Samford University
- Southern Adventist University
- Stevens Institute of Technology
- The College of New Jersey
- University of Central Florida
- University of Central Oklahoma
- University of Findlay
- University of Hartford
- University of Kentucky
- University of La Verne
- Valley Forge Military College
- Washington and Lee University
- Webster University
- West Chester University
- West Virginia Wesleyan College
- Western Governors University
- Wheaton College Illinois
- Whitman College
- Widener University
- William Jewell College
- Winthrop University
- Yeshiva University
CALCULUS II: ACADEMICS
Through the usage of a computer algebra system like LiveMath™ - you will never miss a minus sign again!
Although the driving of a computer algebra system requires some up-front time to learn and master, once completed (rather quickly for most students), the time saved from having to be a "minus sign accountant" adds to the productivity of your study time. If you have ever spent hours looking for that "little numerical error", you know what we mean.
Command of a computer algebra software system is a modern-day necessity of mathematical academics. It is important, however, to retain a meaningful command of paper/pen/pencil manual computations as well. Our blend of curriculum strives for an 80%/20% split between computer algebra usage and manual computation and written skills. With each module in our curriculum, a concluding Literacy Sheet assignment ensures that each student has written mathematical competency in the subject area.
A modern-day study of the topics in Calculus II demands the usage of a computer. Although the learning of integration techniques is meant to support a manual approach to the calculation, the goal is to learn the concepts of the techniques, and to drive the computer algebra tool to computations using those techniques. Writing out long computations on the solution of
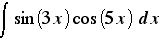
is rather pointless considering the technology available today; but understanding the process and strategy towards computing this antiderivative, and the inherent skills acquired that will generalize to other solution skills, is essential, and the usage of computer algebra technology allows for this study to replace time wasted on multi-page hand calculations.
The proctored final exam is a written exam away from the computer. It is these Literacy Sheet assignments, and the continuing bridge from modern computer algebra software back to classical, manual mathematics that prepares the student from this written final exam.
We do not have any multiple-choice work. We are a real collegiate-level course program - not a "canned" set of multiple-choice question sheets which are common from large publishers and degree-mill schools.
Calculus II - Example Curriculum
Videotext - A Modern Replacement of the Textbook
What is a videotext? It is like a textbook, except instead of being based upon printed information, this "text" is based upon video presentations as the core method of explaining the course topics. Instead of a huge, thick 1000-page Calculus textbook to lug around in your backpack, all of this new "videotext" can be loaded into your iPods or iPhones (and soon, the iPad!).Example Videos are in MP4/H.264 format, which play in most modern browsers without additional software. When additional software is required, a backup Flash player will play the video. As a backup to Flash, you may also use iTunes and/or VLC.
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
Calculus II - Screencast Video Questions
One extremely powerful aspect of the Distance Calculus course technologies is the usage of screencast video (and audio) recordings made by the students and the instructors, exchanged just as easily as emails back and forth.
If a picture is worth a thousand words, then a screencast movie is worth a million words - and saves boatloads of time and effort.
Instead of trying to type out a math question about a particular topic or homework question, the ease of "turning on the screen recorder" and talking and showing your question - in the span of a few minutes - can save hours of time trying to convert your question into a typed (and coherent) narrative question.
Example Student/Instructor Question/Answer Movies
When a student asks a question in a homework notebook, sometimes the best way to explain the answer is via a screen movie. We utilize easy-to-use software to create screen movies with audio so that you can communicate with your instructor "as if they were sitting at the computer with you". Students don't ask questions like this everytime they have a question, but it is a good way to ask questions after text chats aren't working.If a picture is worth a thousand words, and a movie is worth a thousand pictures, then a movie with audio is worth 1000*1000*1000 = 1,000,000,000 (billion) words!
- Student Question Movie Play Video
This screen video was created by a student in the Calculus II course, asking a question about a particular homework problem.
- Instructor Question/Answer Movie Play Video
This screen video was created by the instructor, answering the student's video question.
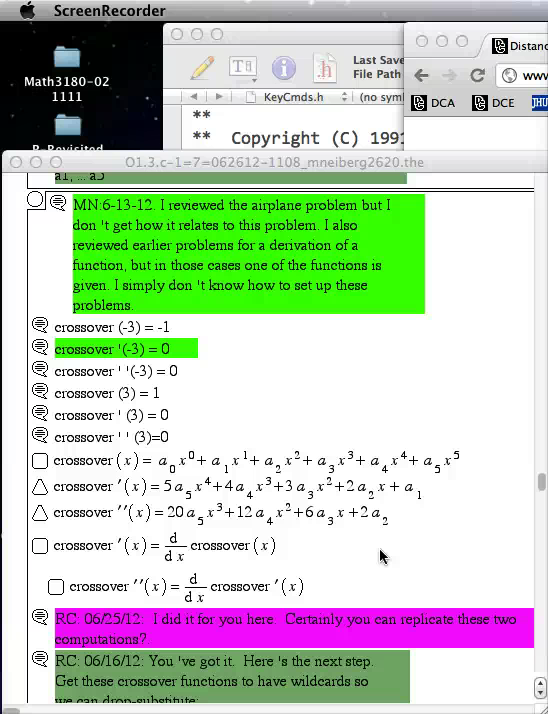
- Student Question Movie Play Video
This screen video was created by a student in the Calculus II course, asking a question about a particular homework problem.
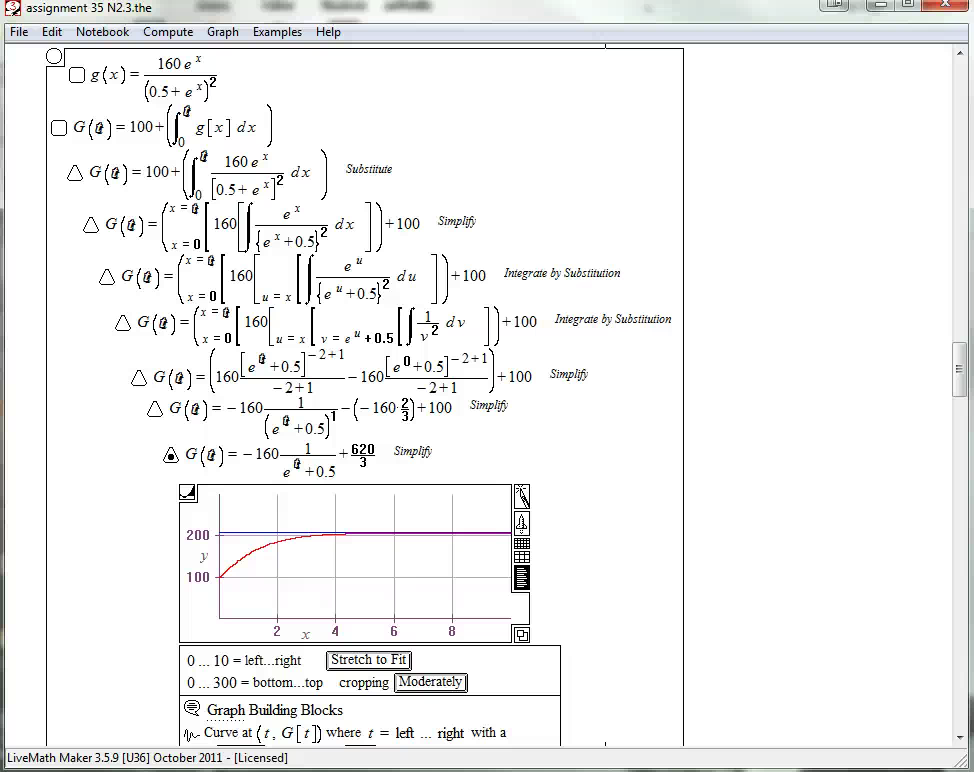
Calculus II - Example Student Work and Grading
The majority of course work occurs via the exchange of LiveMath™ notebooks - think Word Processing Files, but for mathematical computations instead of just text.
The student will "Hand-In" a notebook, and one of the instructors will grade, correct, give feedback, and/or give hints on the work in the notebook, and return the notebook to the student in his/her "GetBack" folder, where the student will view the instructor comments.
Sometimes the notebook is deemed "Complete" on the first revision. Sometimes the notebook must go back and forth between the student and instructor a number of times - 2, 3, 4, 5 times is rather common.
Coupled with the screencast video mechanism, sometimes the instructor or the student will submit a screen movie with the notebook, giving further explanation or questions in audio/video format.
Below are some example notebooks from actual students, showing the progression from starting notebook to completed notebook.
- LiveMath™ Homework Notebook #1 PDF Printout View PDF

- LiveMath™ Homework Notebook #2 PDF Printout View PDF

Distance Calculus - Student Reviews





Date Posted: Apr 10, 2020
Review by: Benjamin T.
Courses Completed: Calculus I
Review: This course provided an excellent chance to learn about Calculus...again. I took calculus in high school, but I learned so much more with this course! It does take a good amount of time to do all the lessons, so definitely keep on top of them, but all the exercises helped me to really understand the material. And the nice thing is you can do it on your own time at home.
Transferred Credits to: Western University of Health Sciences: College of Optometry





Date Posted: Apr 5, 2020
Review by: Catherine M.
Courses Completed: Calculus I
Review: Calculus I from Distance Calculus was wonderful! I took AB Calculus in high school, but I didn't take the AP Calc exam. Instead I took Calculus I with Distance Calculus, and it was so much better! It was a little review of topics, but not really. I really understood calculus when I finished!
Transferred Credits to: University of Chicago





Date Posted: Sep 20, 2020
Review by: Genevieve P.
Courses Completed: Applied Calculus
Review: I found out from my grad school after being accepted that I needed a Calculus course before starting their MBA program. I had less than 6 weeks to do it (and as a non-STEM undergrad no less). The video lectures were informative, the pre-calc refresher was great to get re-conditioned, and the asynchronous format worked so well as I did this at night/weekends after work. I completed it in 4 weeks. Professor Curtis was extremely responsive, graded assignments quickly, and a supportive guide providing constructive feedback to me to excel at the assignments. I highly recommend this course for those who need a pre-req in a hurry or like learning on their own schedule. Thanks, Distance Calculus and Professor Curtis!
Transferred Credits to: Massachusetts Institute of Technology (MIT)
Frequently Asked Questions
Sort of. Calculus 2 (Calculus II) is a notoriously long course, with lots of topics of varying difficulty. Students usually find the Sequence and Series chapters to be the most challenging to master.
Yes. AP Calculus BC is equivalent to the Calculus II (Calculus 2) course.
Yes. Both the Calculus I and Calculus II courses study the Fundamental Theorem of Calculus extensively. The Fundamental Theorem of Calculus is, essentially, that differentiation and integration are inverse operations to each other.
No. Applied Calculus is the lower, lighter, and terminal single-semester Calculus course. You cannot take Calculus II after taking Applied Calculus. If you need to take Calculus II, you may need to go back and take Calculus I, even if you completed Applied Calculus.
Yes, All Distance Calculus courses are offered through Roger Williams University in Providence, Rhode Island, USA, which is regionally accredited (the highest accreditation) through New England Commission of Higher Education (NECHE).
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]