HonorsLinear Algebra For Data Science Online Course for Academic Credit
Honors Linear Algebra is technically part of the undergraduate Calculus sequence, usually taken the sophomore year, but there is almost no Calculus in the course! Linear Algebra is usually considered a more difficult course, especially in a classroom/textbook format. Our Linear Algebra via Distance Calculus is a beautiful course, with masterful use of Mathematica that brings together the topics in a highly visual way, giving the student both theoretical and computational understanding of the very important topics of Linear Algebra, especially for economics, data science, computer science, engineering, and financial mathematics.
| Course Title: | Honors Computational Linear Algebra for Data Science |
| Catalog Number: | DMAT 337 |
| Credits: | 5 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for Honors Computational Linear Algebra for Data Science |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 337 - Honors Computational Linear Algebra for Data Science | |
Nationally, "Honors" courses usually are centered on a mathematically rigorous development of the concepts of calculus, bringing many advanced topics from upper division courses such as Advanced Calculus and Real Analysis into the freshman honors calculus courses. While this may be a worthwhile approach for students who seek to become mathematics majors, it creates, for many students, an inflated level of course difficulty of questionable benefit to related fields of study.
Our approach to Honors courses is built upon a distinctly different educational philosophy:
- Freshman & Sophomore Calculus is NOT the correct math level to increase rigor
We believe that mathematical rigor is learned after exposure to the calculus, in the upper division, after some time and maturing of mathematical thought is allowed to organically develop. No student ever understood the concept of a derivative because the natural numbers were first axiomatically developed. - Honors means DEEPER, not just HARDER
In mathematics, the potential for making any course harder is a rather simple proposition. Work SMARTER, not HARDER mandates that an honors course should not be more difficult just to say it is. A true honors student wants to go deeper into the topics, not flirt with academic demoralization via some mathematical bootcamp experience. - Technical Writing Curriculum
While axiomatic development has its place in upper division math, core improvement of technical writing skills will benefit all students in all disciplines with immediate effect. If calculus is supposed to be mathematical preparation for science, technology, and engineering related fields, then development of technical writing skills should be as important as computational prowess. - Course Term Paper
Each Honors course student will write a 10-20 page term paper on a topic chosen in collaboration with the course instructor, empowering the student to simultaneously improve technical writing skills and deepen knowledge in the student's chosen academic field via a uniquely creative exercise that will transcend the traditional course boundaries.
In summary, our Honors courses go deeper and broader in the curriculum, offer a notch more challenging course work set, and featuring a technical writing curriculum that truly prepares the student for further academics in the sciences.
Completion of DMAT 337 - Honors Linear Algebra for Data Science earns 5 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
Linear Algebra Introductory Videos
Honors Linear Algebra for Data Science Course Introduction
Linear Algebra is a sophomore-level introductory course to the subject.
Traditional approaches to the subject include learning tedious manual computations on matrices, followed by an introduction to a more abstract approach to looking at a class of examples called linear spaces.
Our approach in this course is not a traditional one. In the words of the authors of the curriculum, "This is not your mother's (or father's) linear algebra course", referring to the fact that someone who took an introductory linear algebra course years ago would not recognize much similarity with this course.
Leveraging the high-powered computer algebra and graphing system Mathematica™ by Wolfram Research, the course curriculum Matrices, Geometry, & Mathematica by Davis/Porta/Uhl bypasses the traditional manual calculation tedium, and leapfrogs to a computationally-based, geometric, experimentation-centered approach to the subject. Instead of learning manual computations that are today easily completed by any computer algebra system, this course races into topics that are seldom found in any linear algebra textbook - a quite unique, fresh, and powerful approach to the subject.
Students completing this Matrices, Geometry, & Mathematica curriculum will have a thorough understanding of the geometry of linear algebra, the solutions of linear systems of equations, and the theoretical investigation of the generalized linear spaces concept (although only lightly dabbling in "proofs" - just the right amount for this course level).
Roger Williams University Course Catalog Listing: DMAT 337 - Honors Computational Linear Algebra for Data Science
Course: DMAT 337
Course Title: Honors Computational Linear Algebra for Data Science
Transcript Course Title (30 Characters Max:): Honors Linear Algebra Data Sci
Course Description: An honors-level first course in matrix algebra and linear spaces with emphasis on computational software techniques and geometrical analysis, with applications applicable to data science. Topics include matrices, solutions of systems of linear equations, determinants, linear spaces and transformations, inner products, higher dimensional spaces, inverses and pseudoinverses, rank, Singular Value Decomposition, change of basis, Eigenvalues and Eigenvectors, matrix decomposition and diagonalization, Principal Component Analysis, image and data compression, and an introduction to numerical analysis issues in the subject. Honors courses will include greater breadth and depth of topics, and develop technical writing skills, culminating in a mathematical term paper on an approved topic. [5 Semester Credits]
Prerequisite: Successful completion with grade B or higher in Calculus II or equivalent, or consent of instructor.
E-Textbook: Matrices, Geometry & Mathematica by Davis/Porta/Uhl
Software: Mathematica
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 337 - Honors Computational Linear Algebra for Data Science
DMAT 337 - Honors Computational Linear Algebra for Data Science - Learning Outcomes
- 1. To understand the core connection between matrix algebra and a study of systems of linear equations
- 2. To understand and compute measurements of vectors and their geometry
- 3. To understand and compute core matrix algebra operations and their geometrical interpretations
- 4. To understand and compute the fundamental properties of determinants and inverses of matrices, both for square and non-square generalizations
- 5. To understand and compute Singular Value Decomposition
- 6. To understand and compute the core concept of rank and its variations
- 7. To understand and compute Gaussian elimination and other strategies for finding solutions or approximate solutions to systems of linear equations
- 7. To understand and compute bases, change of bases, spanning and linear independence, kernel and image sets
- 8. To understand and compute the diagonalization of a matrix, both with Singular Value Decomposition, and Eigenvalue - Eigenvector constructions.
- Honors Topics:
- 9.* To understand and compute interpolating polynomials and Fourier fitting and analysis
- 10.* To understand and compute the Gram-Schmidt process in relation to Singular Value Decomposition
- 11.* To understand and compute the diagonalization of a matrix when Eigenvalues are repeated and/or complex.
- 12.* To understand and compute the relationship of matrix diagonalization and dynamical systems of differential equations
- 13.* To understand and compute the Spectral Theorem
- 14.* To understand Principal Component Analysis and additional concepts in data fitting
- 15.* To understand issues concerned with image compression and round-off error
- 16.* To develop mathematical technical writing skills, culminating in a term paper on an approved topic
DMAT 337 - Honors Computational Linear Algebra for Data Science - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. Vectors 2.1. Geometry of Vectors 2.2. Perpendicular Frames 2.3. Curves in 2D: Change of Frames/Basis 2.4. Dot Products 2.5. Cross Products 2.6. Ellipses and Ellipsoids 2.7. Area and Volume 3. Matrices 3.1 Basics 3.2 Transforming Curves 3.3 Matrix Arithmetic 3.4 Translations and Rotations 3.5 Shears 3.6 Linear Transformations 3.7 Inverses 3.8 Determinants 3.9 Transposes 3.10 Matrix Decomposition: Singular Value Decomposition 3.11 Rank 3.12 Projections 3.13 Higher Dimensions 4. Linear Systems 4.1 Conversion to Matrix Notation 4.2 Gaussian Elimination 4.3 Vector Spaces and Subspaces 4.4 Numerical Considerations 4.5 Applications: Least Square Fit 4.6 Spanning Sets; Basis 4.7 Linear Independence 4.8 Pseudo Inverses 4.9 Approximate Solutions 4.10 Null Space and Image Space 4.11* Interpolating Polynomials and Trigonometric Functions: Fourier Fit 4.11* Undetermined Coefficients in Differential Equations Systems 5. Eigenvalues and Eigenvectors 5.1 Diagonalization of a Matrix 5.2 Eigenvalues 5.3 Eigenvectors 5.4 Exponential of a Matrix 6. Principal Data Component Analysis 6.1 Image and Data Compression 6.2 Round-off Error 6.3 Principal Data Component Analysis with SVD 7.* Honors Topics 7.1* Gram-Schmidt Process and Singular Value Decomposition 7.2* 4D Projections 7.3* Non-Real Eigenvalue and Eigenvectors 7.4* Applications to Dynamical Systems 7.5* Spectral Theorem 8.* Mathematical Writing 8.1* Cogent writing 8.2* Mathematical Presentation 8.3* Term Paper Topic and Research
Samples of Linear Algebra Lecture Movies
Honors Linear Algebra for Data Science Examples of the Curriculum
Below are some PDF "print outs" of a few of the Mathematica™ notebooks from Matrices, Geometry, & Mathematica by Davis/Porta/Uhl. Included as well is an example homework notebook completed by a student in the course, demonstrating how the homework notebooks become the "common blackboards" that the students and instructor both write on in their "conversation" about the notebook.
- Sample Curriculum PDF MGM.01.B5 - Basics - 3D Perpendicular Frames
- Sample Curriculum PDF MGM.02.T1 - Tutorials - Hitting with a 2D matrix and visual assessment of the result
- Help Movie Hanging & Aligning
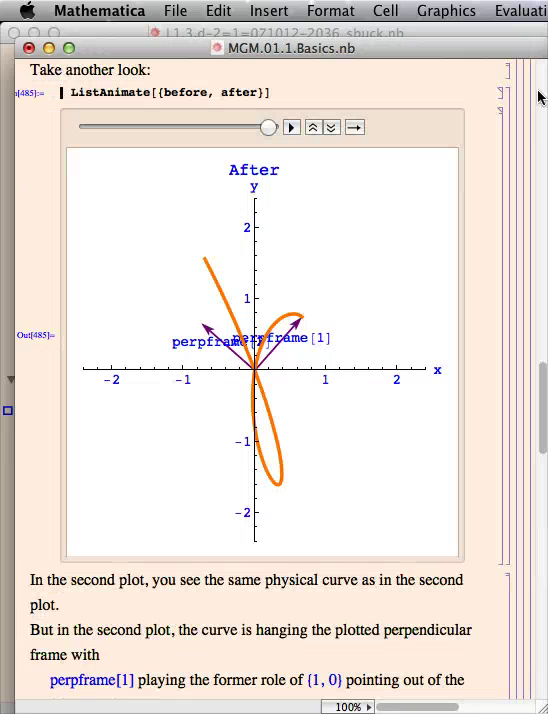
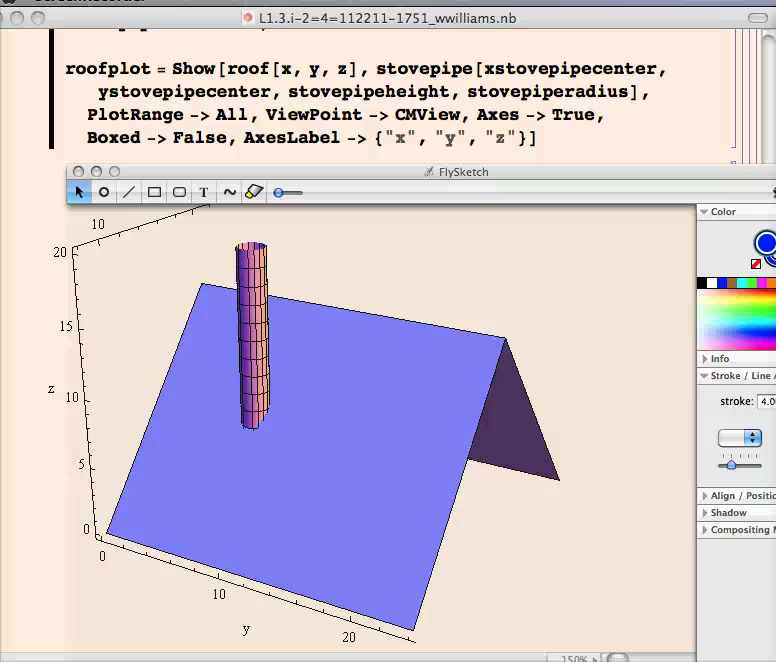
- Help Movie Stovepipe Problem
That Looks Like Programming Code!
Yes, Mathematica™ is a syntax-based computer algebra system - i.e. the instructions to generate the graphs and computations look like a programming language code (which it is).This course is not a course on programming. We do not teach programming, nor do we expect the students to learning programming, or even to know anything about programming. The mathematics is what is important in this course, not the code.
With that tenet in mind, the authors of the Matrices, Geometry, & Mathematica courseware have designed the explanation notebooks (Basics & Tutorials) and the homework notebooks (Give It a Try) in such a way as to make it easy to Copy/Paste from the explanations into the homework notebooks, and make minor changes (obvious ones) to produce the desired similar (but different) output. In this way, we are able to stick strickly to the mathematics at hand, and deal with the programming code as minimally as possible.
Distance Calculus - Student Reviews
Pros:
-- Exceptional Instruction and Support: Dr. Curtis was incredibly responsive and helpful whenever I had questions. The TA was also very supportive, and thanks to their guidance, I was proud to earn a 100% in the course—even without having taken pre-calculus beforehand.
-- Innovative Software Platform: The custom software used in the course made a huge difference for me. I found it intuitive and engaging, and it helped reinforce the concepts in a way traditional textbooks never did.
-- Thorough, Rigorous Curriculum: The structure of the course really pushed me to stay organized and plan ahead. I felt like I was being challenged in all the right ways.
Potential Considerations for Others:
-- Requires Strong Time Management: If you haven’t taken pre-calc, like me, you’ll need to be extra proactive. The course can move quickly if you need, and pacing yourself is essential.
-- Software Learning Curve: While I personally loved the software, students who aren’t comfortable adapting to new digital tools might need a bit of extra time upfront to get used to it.
-- Helpful to Have Supplementary Resources: One improvement might be to offer a short list of "starter resources" (videos, concept overviews, etc.) for students who need a broader intro to calculus before diving in.
Overall, I highly recommend this course to motivated students, especially those comfortable with self-paced learning and open to using new tools. Dr. Curtis is a fantastic instructor, and the course setup really works.
Course Information
Frequent Questions
