Linear Algebra Online Course for Academic Credit
Linear Algebra is technically part of the undergraduate Calculus sequence, usually taken the sophomore year, but there is almost no Calculus in the course! Linear Algebra is usually considered a more difficult course, especially in a classroom/textbook format. Our Linear Algebra via Distance Calculus is a beautiful course, with masterful use of Mathematica that brings together the topics in a highly visual way, giving the student both theoretical and computational understanding of the very important topics of Linear Algebra, especially for economics, data science, computer science, engineering, and financial mathematics.
| Course Title: | Computational Linear Algebra |
| Catalog Number: | DMAT 335 |
| Credits: | 4 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for Computational Linear Algebra |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 335 - Computational Linear Algebra | |
Completion of DMAT 335 - Computational Linear Algebra earns 4 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
Linear Algebra Introductory Videos
Linear Algebra Course Introduction
Linear Algebra is a sophomore-level introductory course to the subject.
Traditional approaches to the subject include learning tedious manual computations on matrices, followed by an introduction to a more abstract approach to looking at a class of examples called linear spaces.
Our approach in this course is not a traditional one. In the words of the authors of the curriculum, "This is not your mother's (or father's) linear algebra course", referring to the fact that someone who took an introductory linear algebra course years ago would not recognize much similarity with this course.
Leveraging the high-powered computer algebra and graphing system Mathematica™ by Wolfram Research, the course curriculum Matrices, Geometry, & Mathematica by Davis/Porta/Uhl bypasses the traditional manual calculation tedium, and leapfrogs to a computationally-based, geometric, experimentation-centered approach to the subject. Instead of learning manual computations that are today easily completed by any computer algebra system, this course races into topics that are seldom found in any linear algebra textbook - a quite unique, fresh, and powerful approach to the subject.
Students completing this Matrices, Geometry, & Mathematica curriculum will have a thorough understanding of the geometry of linear algebra, the solutions of linear systems of equations, and the theoretical investigation of the generalized linear spaces concept (although only lightly dabbling in "proofs" - just the right amount for this course level).
Roger Williams University Course Catalog Listing: DMAT 335 - Computational Linear Algebra
Course: DMAT 335
Course Title: Computational Linear Algebra
Transcript Course Title (30 Characters Max:): Comp Linear Algebra
Course Description: A first course in matrix algebra and linear spaces with emphasis on computational software techniques and geometrical analysis. Topics include matrices, solutions of systems of linear equations, determinants, linear spaces and transformations, inner products, higher dimensional spaces, inverses and pseudoinverses, rank, Singular Value Decomposition, bases, rank, Eigenvalues and Eigenvectors, matrix decomposition and diagonalization. [4 Semester Credits]
Prerequisite: Successful completion (C- or higher) of Calculus II or equivalent, or consent of instructor.
E-Textbook: Matrices, Geometry & Mathematica by Davis/Porta/Uhl
Software: Mathematica
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 335 - Computational Linear Algebra
DMAT 335 - Computational Linear Algebra - Learning Outcomes
- 1. To understand the core connection between matrix algebra and a study of systems of linear equations
- 2. To understand and compute measurements of vectors and their geometry
- 3. To understand and compute core matrix algebra operations and their geometrical interpretations
- 4. To understand and compute the fundamental properties of determinants and inverses of matrices, both for square and non-square generalizations
- 5. To understand and compute Singular Value Decomposition
- 6. To understand and compute the core concept of rank and its variations
- 7. To understand and compute Gaussian elimination and other strategies for finding solutions or approximate solutions to systems of linear equations
- 7. To understand and compute bases, change of bases, spanning and linear independence, kernel and image sets
- 8. To understand and compute the diagonalization of a matrix, both with Singular Value Decomposition, and Eigenvalue - Eigenvector constructions.
DMAT 335 - Computational Linear Algebra - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. Vectors 2.1. Geometry of Vectors 2.2. Perpendicular Frames 2.3. Curves in 2D: Change of Frames/Basis 2.4. Dot Products 2.5. Cross Products 2.6. Ellipses and Ellipsoids 2.7. Area and Volume 3. Matrices 3.1 Basics 3.2 Transforming Curves 3.3 Matrix Arithmetic 3.4 Translations and Rotations 3.5 Shears 3.6 Linear Transformations 3.7 Inverses 3.8 Determinants 3.9 Transposes 3.10 Matrix Decomposition: Singular Value Decomposition 3.11 Rank 3.12 Projections 3.13 Higher Dimensions 4. Linear Systems 4.1 Conversion to Matrix Notation 4.2 Gaussian Elimination 4.3 Vector Spaces and Subspaces 4.4 Numerical Considerations 4.5 Applications: Least Square Fit 4.6 Spanning Sets; Basis 4.7 Linear Independence 4.8 Pseudo Inverses 4.9 Approximate Solutions 4.10 Null Space and Image Space 5. Eigenvalues and Eigenvectors 5.1 Diagonalization of a Matrix 5.2 Eigenvalues 5.3 Eigenvectors 5.4 Exponential of a Matrix
Legacy Course Connection
Legacy Distance Calculus Course:
DMAT 331 - Linear Algebra
In 2023, Distance Calculus introduced a new catalog of courses. The connection between the old courses and the new courses are given here:
Legacy Course Description: Presents matrices, determinants, vector spaces, linear transformations, eigenvectors and eigenvalues, diagonalization, solution of systems of linear equations by the Gauss-Jordan method, and applications. (3 credits)
| Common Completion Timelines for DMAT 335 - Linear Algebra | ||||
| Hours Dedicated | Math Skills | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-10 hours/week | Weaker | 1-2 hours/day | 16 weeks | Reasonable |
| 7-12 hours/week | Modest | 2-3 hours/day | 12 weeks | Reasonable |
| 10-15 hours/week | Stronger | 3-4 hours/day | 8 weeks | Reasonable |
| 15-20 hours/week | Strong | 5-6 hours/day | 6 weeks | Stretched |
| 20-25 hours/week | Strong | 5-7 hours/day | 4 weeks | Stretched |
| 25-35 hours/week | Strong | 6-8 hours/day | 3 weeks | World's Record |
Time commitments are important for success in an online Linear Algebra course for college credit from Distance Calculus. There are no fixed due dates in the Distance Calculus online courses, so it is important that students instead set their schedules for a dedicated amount of time towards the coursework.
It is also very important to consider that going faster through a course is DIRECTLY DEPENDENT upon your math skill level, and your successful engagement of the course. We require that you complete the course in a Mastery Learning format. If you are struggling with the course content, or trying to go too fast where the quality of your submitted work is suffering, then the instructors will force a slow-down of your progress through the course, even if you have fixed deadlines.
Samples of Linear Algebra Lecture Movies
Linear Algebra Examples of the Curriculum
Below are some PDF "print outs" of a few of the Mathematica™ notebooks from Matrices, Geometry, & Mathematica by Davis/Porta/Uhl. Included as well is an example homework notebook completed by a student in the course, demonstrating how the homework notebooks become the "common blackboards" that the students and instructor both write on in their "conversation" about the notebook.
- Sample Curriculum PDF MGM.01.B5 - Basics - 3D Perpendicular Frames
- Sample Curriculum PDF MGM.02.T1 - Tutorials - Hitting with a 2D matrix and visual assessment of the result
- Help Movie Hanging & Aligning
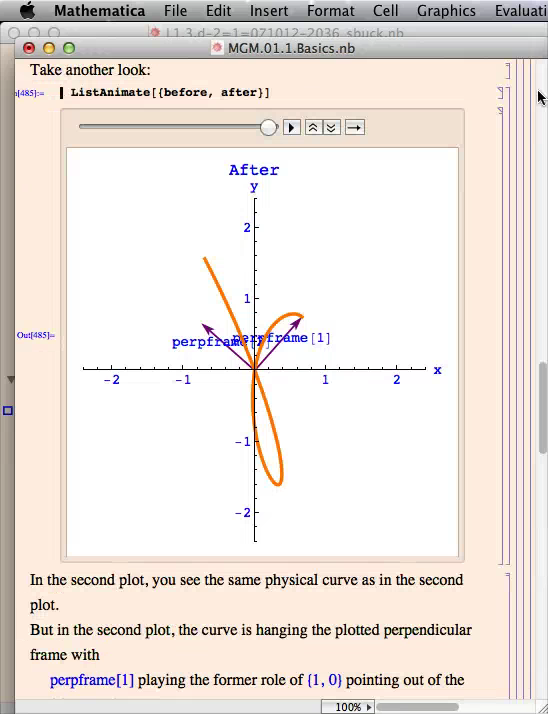
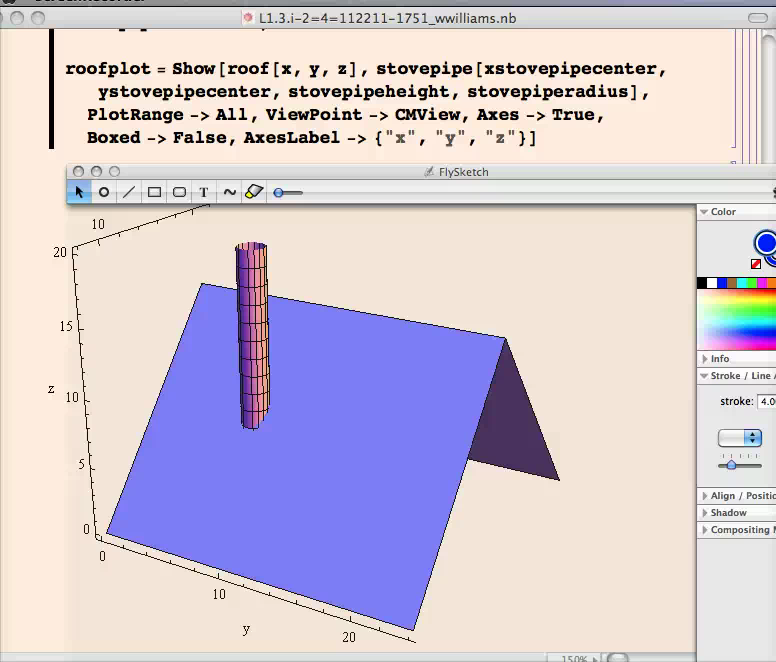
- Help Movie Stovepipe Problem
That Looks Like Programming Code!
Yes, Mathematica™ is a syntax-based computer algebra system - i.e. the instructions to generate the graphs and computations look like a programming language code (which it is).This course is not a course on programming. We do not teach programming, nor do we expect the students to learning programming, or even to know anything about programming. The mathematics is what is important in this course, not the code.
With that tenet in mind, the authors of the Matrices, Geometry, & Mathematica courseware have designed the explanation notebooks (Basics & Tutorials) and the homework notebooks (Give It a Try) in such a way as to make it easy to Copy/Paste from the explanations into the homework notebooks, and make minor changes (obvious ones) to produce the desired similar (but different) output. In this way, we are able to stick strickly to the mathematics at hand, and deal with the programming code as minimally as possible.
Distance Calculus - Student Reviews
The course materials are fantastic. If you are a student sitting on the fence, trying to decide between a normal classroom class or Distance Calculus classes with Livemath and Mathematica, my choice would be the Distance Calculus classes every time. The Distance Calculus classes are more engaging. The visual aspects of the class notebooks are awesome. You get the hand calculation skills you need.
The best summary I can give is to say, given the opportunity, I would put my own son's math education in Dr. Curtis's hands.
One of the best math classes I have ever taken. The lessons made the failures of my previous professors very apparent. In a few short minutes, things that I used to struggle with just clicked. This professor is top notch and really wants you to understand how to use the material.
NEGATIVES:
The SOFTWARE is extremely frustrating. Even after taking the time to learn, there are countless glitches. You learn to work around them, and overall, the software makes the math convenient, but its failures are sorely felt throughout the course. Make sure you save often as it crashes regularly, especially with graphs.
The assignments are easy enough but some of them don't line up with the taught material. Be prepared to do some of your own independent research to get a deeper understanding of why things are the way they are.
Course Information
Frequent Questions
Frequently Asked Questions
Yes, most definitely. Linear Algebra is one of the core courses needed for starting any degree program in Data Science
Yes, Calculus II is the prequisite for the Linear Algebra course, but interestingly no Calculus is used in the Linear Algebra course!
4-6 Weeks is a very fast but reasonable pace to finish the Linear Algebra course.
Anytime - Enrollment for Distance Calculus courses is on-going - enroll and start the course on the same day
Linear Algebra is quite different from Calculus, but it is not a harder course than Calculus II. Some students find Linear Algebra to be easier than Calculus, while other students find Linear Algebra to be more challenging than Calculus.
