Applied Calculus Online Course for Academic Credit
"Applied Calculus" - DMAT 201 - Calculus for Business - is best described as a "single college-level course in differential and integral calculus". This type of single-semester course has many equivalent names:
- Applied Calculus
- Business Calculus
- Survey of Calculus
- Liberal Arts Calculus
- Calculus for Management or Social Science or ...
- Calculus for Biology
| Course Title: | Applied Calculus for Business |
| Catalog Number: | DMAT 201 |
| Credits: | 3 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for Applied Calculus for Business |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 201 - Applied Calculus for Business | |
Sometimes Applied Calculus is referred to as "Junior Calculus" or even "Baby Calc" - distinguishing Applied Calculus as the lower track of Calculus, in comparision to the higher track of Engineering-level Calculus I.
Completion of DMAT 201 - Calculus for Business earns 3 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
DMAT 201 - Calculus for Business is offered in the Fall, Winter, Spring, and Summer semesters with "revolving enrollment", which means you may enroll at any time, and start your course whenever you wish, independent of the traditional academic calendar.
Applied Calculus Course Information Video
Applied Calculus via Distance Calculus
Video Time: 29 minutes
What is Distance Calculus?
Video Time: 2 minutes
Applied Calculus vs STEM Calculus I
Video Time: 17 minutes
How FAST To Complete Distance Calculus Course?
Video Time: 28 minutes
Different Names for Applied Calculus
- Applied Calculus
- Business Calculus
- Survey of Calculus
- Liberal Arts Calculus
- Calculus for Management or Social Science or ...
- Calculus for Biology
- Calculus for Life Sciences
- Brief Calculus
Lower Applied Calculus vs. Higher Engineering STEM Calculus I
Both Applied Calculus and (Engineering) Calculus I provide an introduction to differential and integral calculus.
Applied Calculus provides a lighter, more general introduction to the introductory topics of Calculus, while the higher Calculus I course expects students to have strong fundamentals the limit definition, definition of continuity, derivatives of functions, integrals, and applications of calculus to more difficult and challenging problem sets, in preparation for continuation to the higher Calculus II course in the first year Calculus sequence. Applied Calculus is "a notch or two easier" than the Engineering Calculus I course
Applied Calculus does not include nor require trigonometry. High School Algebra II is sufficient prerequisite for Applied Calculus, while the higher Calculus I course requires College Algebra, Trigonometry, and/or Precalculus.
The main topical differences between the lower Applied Calculus and the higher (Engineering) Calculus I course are described in the table below.
| Topic | Applied Calculus | Calculus I |
|---|---|---|
| Trigonometry | No | Yes |
| Analytical Geometry | No | Conic Sections, Parametric Functions |
| Functions | Polynomials, Roots, Exponential, Logarithmic | Polynomials, Roots, Exponential, Logarithmic, Trigonometric, Composite, Integral Functions |
| Limits, Definition of Continuity | Mainly Graphical, Numerical | Algebraic, Graphical, Numerical |
| Derivatives | Simple Algebraic Rules | Rigorous Rule Development, Application |
| Applications of Calculus | Economics, Finance, Easier | Physics, Economics, Rates, Challenging |
| Introduction to Differential Equations | No | Yes |
| Derivatives and Integrals of Parametric Curves/Functions | No | Yes |
| Displacement, Velocity, Acceleration | Minimal | Yes |
| Integration | Basic Integration Rules | Algebraic Integration, Integral Functions, Integration via Substitution, Preparation for Calculus II |
The Applied Calculus course does include more applications to business, finance, economics, etc. than does the Engineering Calculus course.
Roger Williams University Course Catalog Listing: DMAT 201 - Applied Calculus for Business
Course: DMAT 201
Course Title: Applied Calculus for Business
Transcript Course Title (30 Characters Max:): Calculus for Business
Course Description: A single course in differential and integral calculus for management and business with emphasis on computational techniques and graphical analysis. Topics include a study of the algebraic and numerical aspects of linear, quadratic, polynomial, exponential, and logarithmic functions, function growth, derivative analysis and optimization, integration, applications to economics, partial derivatives and higher dimensional optimization, and the Fundamental Theorem of Calculus. [3 Semester Credits]
Prerequisite: Successful completion of 3 years high school mathematics (C- or higher) or instructor consent.
E-Textbook: “Business Calculus & LiveMath” by Robert R. Curtis, Ph.D., adapted from Davis/Porta/Uhl “Calculus&Mathematica” courseware series
Software: LiveMath
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 201 - Applied Calculus for Business
DMAT 201 - Applied Calculus for Business - Learning Outcomes
- 1. To identify, manipulate, and understand the algebraic, numerical, and graphical fundamentals of linear, polynomial, exponential, logarithmic, and rational polynomial functions
- 2. To understand and compute numerical, and graphical limits at finite and infinite values
- 3. To understand and compute the fundamental concept of the derivative
- 4. To understand and compute various measurements of growth of a function
- 5. To algebraically compute derivatives of common functions using summation, product, quotient, and chain rules for derivatives
- 7. To understand and compute optimization of functions using derivatives, finding critical values
- 8. To understand and compute the second derivative
- 9. To understand and calculate numerically and graphically the core concepts of the integral for applications to signed area measurements;
- 10. To compute numerically, algebraically, and graphically integrals of a variety of functions;
- 11. To algebraically compute integrals of basic polynomial and exponential functions, with an introduction to the algebraic substitution technique;
- 12. To use the tools of differential and integral calculus in various applications in business and finance
- 13. To understand and compute the Fundamental Theorem of Calculus
- 14. To understand and compute partial derivatives of multivariable functions, to begin study of optimization in higher dimensions.
- 15. To utilize computer algebra and graphing software to amplify traditional manual computation techniques.
DMAT 201 - Applied Calculus for Business - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. The Big Picture 2.1 Solving (easy) equations in 1 variable. 2.2 What if you can't solve for x? 2.3 Finding solutions numerically 2.4 Finding solutions graphically 2.5 Solving equations of more than 1 variable 3. Functions 3.1 Function notation 3.2 Data sets 3.3 Graphing functions 3.4 Data sets and smooth curves 3.5 Domain and Range 3.6 Algebraic combinations of functions 4. Linear Functions 4.1 Algebraic definition 4.2 Slope 4.3 Graphing linear functions by hand 4.4 Properties of linear functions 4.5 Linear data sets 5. Quadratic Functions 5.1 Algebraic definition 5.2 Graphing and Properties of Quadratic Functions 5.3 Solving quadratic equations algebraically: Factoring 5.4 Solving quadratic equations algebraically: Quadratic formula 5.5 Solving quadratic equations numerically and graphically 6. Power and Polynomial Functions 6.1 Algebraic definition 6.2 Graphing and Properties of Polynomial Functions 6.3 Solving polynomial equations algebraically: factoring 6.4 Solving polynomial equations numerically and graphically 6.5 Radicals and fractional exponents 7. Rational Polynomial Functions 7.1 Algebraic definition 7.2 Graphing and Properties of Rational Polynomial Functions 7.3 Solving rational polynomial equations algebraically: factoring 8. Exponential Functions 8.1 Algebraic definition 8.2 Graphing and Properties of Exponential Functions 8.3 Solving exponential equations numerically and graphically 8.4 Exponential Growth and Applications 8.5 Data sets and exponential functions 9. Logarithmic Functions 9.1 Inverse Functions 9.2 Algebraic Definition 9.3 Graphing and Properties of Logarithmic Functions 9.4 Solving exponential and logarithmic equations algebraically 9.5 Solving logarithmic equations numerically and graphically 9.6 Logarithmic Growth and Applications 9.7 Data sets and logarithmic functions 10. Growth: Preparing for the Derivative 10.1 Growth of Linear Functions 10.2 Growth of Power Functions 10.3 Growth of Exponential Functions 10.4 Dominance of Growth of Functions 10.5 Percentage Growth of Functions 10.6 Global Scale: Infinite Limits 10.7 Data Functions and Interpolation 10.8 Approximation of Functions by Linear Functions 11. Exponential Functions and Natural Logarithms 11.1 e = Euler's Number 11.2 Natural Logarithm 11.3 Growth Analysis 11.4 Applications: Carbon Dating 11.5 Percentage Growth and Steady Growth of Exponential Functions 11.6 Data Functions and Logarithmic Analysis 11.7 Applications: Compound Growth Rates 11.8 Applications: World Population 11.9 Applications: Finance and Interest Rates 12. The Derivative of Polynomial, Exponential, Logarithmic, and Fractional Powers 12.1 Instantaneous Growth Rates 12.2 Definition of the Derivative 12.3 Computing the Derivative Graphically 12.4 Computing the Derivative Algebraically 12.5 Computing the Derivative Numerically 12.6 Average Growth Rate vs. Instantaneous Growth Rate 12.7 Applications of the Derivative: Spread of Disease 12.8 Finding Maxima and Minima of Functions 12.9 Relating a Function and Its Derivative 13. Computing Derivatives 13.1 Sum, Difference, Product, Quotient Rule 13.2 Chain Rule 13.3 Instantaneous Percentage Growth 13.4 Growth Dominance 14. Using Derivatives 14.1 Finding Maxima and Minima 14.2 Finding Good Representative Plots 14.3 The Second Derivative 15. Integration 15.1 Measuring Area Under a Curve 15.2 Definition of the Integral 15.3 Properties of Integrals, Symmetry 15.4 Integrals of Data Functions 15.5 Numerical Methods: Rectangles, Trapezoids 15.6 Undefined Integrals 15.7 Numerical Calculation of Integrals 16. Fundamental Theorem of Calculus 16.1 Derivative of an Integral 16.2 Integral of a Derivative 16.3 Fundamental Formula 16.4 Properties of Integrals 16.5 Indefinite Integrals and Antiderivatives 16.6 u-Substitution 17. Higher Dimensions 17.1 Multivariable Functions 17.2 Partial Derivatives 17.3 Tangent Planes 17.4 Optimization
Legacy Course Connection
Legacy Distance Calculus Course:
DMAT 207 - Applied Calculus
In 2023, Distance Calculus introduced a new catalog of courses. The connection between the old courses and the new courses are given here:
Legacy Course Description: This course covers fundamental notions of differentiation and integration of algebraic, exponential and logarithmic functions, with problems drawn from principally from business situations. Topics include optimization, related rates, and simple applications and methods of integration. While covering traditional analytic methods, this course also emphasizes graphical and numerical approaches. This course may not be taken for credit by mathematics majors, minors or core concentrators. No credit will be given to students who have previously received credit for MATH 213. (3 credits)
Nearly all collegiate students have completed "high school algebra". There is no mathematics placement exam. The Applied Calculus course starts with a very thorough "warm up" module on the important topics of high school algebra, with the added usage of the LiveMath software, which makes for an excellent "refresher" for student who have maybe be away from academic mathematics for some time.
Will Applied Calculus Suffice For Your Program?
The keywords to look for in your academic program's description is
Academic programs that usually will accept the lower Applied Calculus course include:
- MBA & Business Schools
Many MBA & EMBA programs accept Applied Calculus to satisfy their calculus course requirement. - Pharmacy, Nursing, or Pre-Med Schools
- Architecture
- Baccelaureate General Education Requirements
- Other Graduate School Programs
- Primary/Secondary Education Teacher Certification
Academic programs that usually require the higher (Engineering) Calculus I course include:
- Science Majors
Physics, Mathematics, Engineering, Computer Science, Chemistry - Economics Majors/Degrees
Programs in Economics tend to be more mathematically oriented, and usually require Calculus I and beyond - Special Military Training
Advanced military training programs, such as Test Pilot School, usually the higher Calculus I course
Transferring Credits vs. Satisfying Program Prerequisites
Many of our Applied Calculus students are seeking to satisfy the prerequisites for a graduate program of study, which is distinctly different than planning to transfer academic credits to a home institution. Some of the differences include:
- Prerequisite Satisfaction: Minimal Grade
Students using the Applied Calculus course to satisfy a prerequisite in another academic program will be required to achieve a minimal grade. For some programs the minimal required grade is a "B", and for others a "C" grade will suffice. - Prerequisite Satisfaction: Course Approval
For Prerequisite Satisfaction, often only the graduate program (usually an admissions officer) must give approval for usage of the Distance Calculus course. For transferring of academic credits, often others, such as the Registrar, must also give approval to transferring credits. - Transferring Credits: Grades May or May Not Transfer
When Transferring Credits, many institutions will accept the academic credits in transfer, but not the letter grade earned. In these cases, earning an "A" in the course is no different than earning a "B" or a "C". Often this type of situation gives the student guidance on which Grade Path to choose for Distance Calculus.
In either case, it is important to check with your graduate program to make sure the Applied Calculus course will satisfy their prerequisite requirements, and to make sure the Distance Calculus course is acceptable to them.
Applied Calculus Course Content & Syllabus
The Applied Calculus course provides a general (and lighter) introduction to beginning calculus.
- Intensive Algebra Refresher
Applied Calculus starts with an intensive 20 assignment refresher of high school Algebra I/II, starting from scratch with solving basic equations, ranging then to functions, linear equations, polynomials, and then exponential and logarithmic functions. This refresher aids students who have been away from academics for a while, as well as students with weaker mathematical backgrounds. For students with stronger math backgrounds, this refresher can be completed very quickly, and provides an excellent platform on which to learn the computer algebra software. - Introduction to Differential Calculus
Applied Calculus begins with investigating the phenomena of growth of the various types of functions, culminating with the derivative as a measurement of growth. Algebraic rules for computing derivatives of functions are explored and utilized. Applications of the derivative to "max/min" problems are the final set of topics in the study of differential calculus. - Introduction to Integral Calculus
Applied Calculus studies the connection between integrals as measurement of signed area of regions defined by function curves, concentrating on the graphical and numerical aspects of integrals. Algebraic methods for computing basic integrals, followed by the introduction of the Fundamental Theorem of Calculus, conclude the course. - Application of Calculus
Applied Calculus is less about "rigourous calculus development" and more about learning various topics to study with the tools of Calculus - mathematical models involving calculus: applications of calculus in finance, applications of calculus in computing area and volume, applications of calculus in physics, applications of calculus in epidemiology. This Applied Calculus course is not "applied" in the sense of only being about these applications, but there are many problem sets about such applications so students learn working knowledge of how calculus is applied in many disciplines.
Applied Calculus - Academic Caveats
Some issues to consider when determining if Applied Calculus is for you.
- Terminal Course
Applied Calculus does not lead to the higher Calculus sequence, and is not equivalent to the higher Calculus I course. Applied Calculus is usually the last math course a student takes as an undergraduate. - No Trigonometry
Applied Calculus does not include nor require Trigonometry. If your academic program requires a calculus course that includes trigonometry, you need to take the Calculus I course instead. - No Multivariable Calculus
Applied Calculus does not branch into the multivariable calculus topics - required by some majors/programs, especially Economics. If you need Multivariable/3D Calculus topics, you'll need to go through the higher Calculus I/II + Multivariable Calculus sequence.
Applied Calculus Student Academic Goals
One way to determine if Applied Calculus is the right course for you is to align yourself with examples of student profiles we usually encounter.
- Prepare for MBA or Other Graduate Program
Many graduate programs, such as MBA's, have prerequisites that include "a single college-level Calculus course". The majority of our Applied Calculus students are seeking to satisfy such prerequisite requirements prior to starting their graduate school program. Our MBA-bound students tend to be highly-focused, goal-oriented students who complete their course work under very tight deadlines. - Pharmacy, Nursing, Pre-Med
Often these academic and training programs require "a single college-level Calculus course" as a prerequisite. Many students in these programs have strong mathematical skills, which aid them in completing the Applied Calculus course quickly. Some students in this category do have weaker mathematical backgrounds, requiring more time to achieve mastery and success in the Applied Calculus course. - General Education Requirement
Many students have "one more class" to finish to earn their baccelaureate degree, and Applied Calculus fits the bill for them.
Warning: Many colleges/universities have a senior residency requirement where the last set of credits (usually 20-30 credits) must be completed at the college/university granting the degree, and cannot be "transferred in" from another school. Make sure you check with your college/university about such rules. - Teacher Re-Certification
Primary and secondary educators often are required to take courses for their certification and/or re-certification programs.
Warning: Distance Calculus courses do not carry graduate-level credits. Some recertification programs require their teachers to complete graduate level credits. Calculus courses are inherently undergraduate-level courses.
Calculus for Business Learning Outcomes
- To identify, manipulate, and understand the algebraic, numerical, and graphical fundamentals of linear, polynomial, exponential, logarithmic, and rational polynomial functions
- To understand and compute numerical, and graphical limits at finite and infinite values
- To understand and compute the fundamental concept of the derivative
- To understand and compute various measurements of growth of a function
- To algebraically compute derivatives of common functions using summation, product, quotient, and chain rules for derivatives
- To understand and compute optimization of functions using derivatives, finding critical values
- To understand and compute the second derivative
- To understand and calculate numerically and graphically the core concepts of the integral for applications to signed area measurements;
- To compute numerically, algebraically, and graphically integrals of a variety of functions;
- To algebraically compute integrals of basic polynomial and exponential functions, with an introduction to the algebraic substitution technique;
- To use the tools of differential and integral calculus in various applications in business and finance
- To understand and compute the Fundamental Theorem of Calculus
- To understand and compute partial derivatives of multivariable functions, to begin study of optimization in higher dimensions.
- To utilize computer algebra and graphing software to amplify traditional manual computation techniques.
DMAT 201 - Calculus for Business - Syllabus
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. The Big Picture 2.1 Solving (easy) equations in 1 variable. 2.2 What if you can’t solve for x? 2.3 Finding solutions numerically 2.4 Finding solutions graphically 2.5 Solving equations of more than 1 variable 3. Functions 3.1 Function notation 3.2 Data sets 3.3 Graphing functions 3.4 Data sets and smooth curves 3.5 Domain and Range 3.6 Algebraic combinations of functions 4. Linear Functions 4.1 Algebraic definition 4.2 Slope 4.3 Graphing linear functions by hand 4.4 Properties of linear functions 4.5 Linear data sets 5. Quadratic Functions 5.1 Algebraic definition 5.2 Graphing and Properties of Quadratic Functions 5.3 Solving quadratic equations algebraically: Factoring 5.4 Solving quadratic equations algebraically: Quadratic formula 5.5 Solving quadratic equations numerically and graphically 6. Power and Polynomial Functions 6.1 Algebraic definition 6.2 Graphing and Properties of Polynomial Functions 6.3 Solving polynomial equations algebraically: factoring 6.4 Solving polynomial equations numerically and graphically 6.5 Radicals and fractional exponents 7. Rational Polynomial Functions 7.1 Algebraic definition 7.2 Graphing and Properties of Rational Polynomial Functions 7.3 Solving rational polynomial equations algebraically: factoring 8. Exponential Functions 8.1 Algebraic definition 8.2 Graphing and Properties of Exponential Functions 8.3 Solving exponential equations numerically and graphically 8.4 Exponential Growth and Applications 8.5 Data sets and exponential functions 9. Logarithmic Functions 9.1 Inverse Functions 9.2 Algebraic Definition 9.3 Graphing and Properties of Logarithmic Functions 9.4 Solving exponential and logarithmic equations algebraically 9.5 Solving logarithmic equations numerically and graphically 9.6 Logarithmic Growth and Applications 9.7 Data sets and logarithmic functions 10. Growth: Preparing for the Derivative 10.1 Growth of Linear Functions 10.2 Growth of Power Functions 10.3 Growth of Exponential Functions 10.4 Dominance of Growth of Functions 10.5 Percentage Growth of Functions 10.6 Global Scale: Infinite Limits 10.7 Data Functions and Interpolation 10.8 Approximation of Functions by Linear Functions 11. Exponential Functions and Natural Logarithms 11.1 e = Euler’s Number 11.2 Natural Logarithm 11.3 Growth Analysis 11.4 Applications: Carbon Dating 11.5 Percentage Growth and Steady Growth of Exponential Functions 11.6 Data Functions and Logarithmic Analysis 11.7 Applications: Compound Growth Rates 11.8 Applications: World Population 11.9 Applications: Finance and Interest Rates 12. The Derivative of Polynomial, Exponential, Logarithmic, and Fractional Powers 12.1 Instantaneous Growth Rates 12.2 Definition of the Derivative 12.3 Computing the Derivative Graphically 12.4 Computing the Derivative Algebraically 12.5 Computing the Derivative Numerically 12.6 Average Growth Rate vs. Instantaneous Growth Rate 12.7 Applications of the Derivative: Spread of Disease 12.8 Finding Maxima and Minima of Functions 12.9 Relating a Function and Its Derivative 13. Computing Derivatives 13.1 Sum, Difference, Product, Quotient Rule 13.2 Chain Rule 13.3 Instantaneous Percentage Growth 13.4 Growth Dominance 14. Using Derivatives 14.1 Finding Maxima and Minima 14.2 Finding Good Representative Plots 14.3 The Second Derivative 15. Integration 15.1 Measuring Area Under a Curve 15.2 Definition of the Integral 15.3 Properties of Integrals, Symmetry 15.4 Integrals of Data Functions 15.5 Numerical Methods: Rectangles, Trapezoids 15.6 Undefined Integrals 15.7 Numerical Calculation of Integrals 16. Fundamental Theorem of Calculus 16.1 Derivative of an Integral 16.2 Integral of a Derivative 16.3 Fundamental Formula 16.4 Properties of Integrals 16.5 Indefinite Integrals and Antiderivatives 16.6 u-Substitution 17. Higher Dimensions 17.1 Multivariable Functions 17.2 Partial Derivatives 17.3 Tangent Planes 17.4 Optimization
Applied Calculus Example Student Profiles
Case 1: MBA-Bound Student Needs Applied Calculus
Sally just got her acceptance letter from her MBA graduate school, but with notification that she needs to finish "a single collegiate-level differential and integral calculus course" by the start of MBA courses.How fast can Sally finish the DMAT 201 - Applied Calculus course?
MBA students tend to be highly-motivated and deadline-centered students, ready to "do what it takes" to get finished by the required date. Here are some scenarios for Sally:
| Common Completion Timelines for DMAT 201 - Applied Calculus for Business | ||||
| Hours Per Week Dedicated | Math Skills | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-10 hours/week | Weaker | 1-2 hours/day | 16 weeks | Reasonable |
| 7-12 hours/week | Modest | 2-3 hours/day | 12 weeks | Reasonable |
| 10-15 hours/week | Stronger | 3-4 hours/day | 8 weeks | Reasonable |
| 15-20 hours/week | Strong | 5-6 hours/day | 6 weeks | Stretched |
| 20-25 hours/week | Strong | 5-7 hours/day | 4 weeks | Stretched |
| 20-25 hours/week | Strong | 6-8 hours/day | 3 weeks | Unreasonable, But Has Been Done |
| 30-40 hours/week | Very Strong | 8-10 hours/day | 2 weeks | Unreasonable, But Has Been Done |
| 40-50 hours/week | Very Strong | 10-12 hours/day | 9 days | World's Record |
Time commitments are important for success in an online Applied Calculus course for college credit from Distance Calculus. There are no fixed due dates in the Distance Calculus online courses, so it is important that students instead set their schedules for a dedicated amount of time towards the coursework.
It is also very important to consider that going faster through a course is DIRECTLY DEPENDENT upon your math skill level, and your successful engagement of the course. We require that you complete the course in a Mastery Learning format. If you are struggling with the course content, or trying to go too fast where the quality of your submitted work is suffering, then the instructors will force a slow-down of your progress through the course, even if you have fixed deadlines.
Case 2: Pharmacy Student Needs Applied Calculus
Marc is planning to go to Pharmacy School in a few months, and needs to finish the Applied Calculus course prior to the start of school. Marc has been away from academic mathematics for many years, and does not have a strong mathematics background, but makes up for such weaknesses with drive, energy, and dedication to achieving his goals.How fast can Marc finish the DMAT 201 - Applied Calculus course?
Marc will need to plan for extra time, especially at the beginning of the course, to get back into the swing of academic mathematics. The high school algebra review portion of the course (20 assignments) will be time well spent for Marc, as he revisits topics from high school that previously he did not have much success with. Marc is able to dedicate himself to the task, and is able to move more quickly through the Calculus curriculum (50 assignments). Here are some scenarios for Marc:
| Common Completion Timelines for DMAT 201 - Applied Calculus | ||||
| Hours Per Week Dedicated | Math Skills | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 8-10 hours/week | Weaker | 1-2 hours/day | 15 weeks | Reasonable |
| 15-20 hours/week | Weaker | 2-3 hours/day | 10 weeks | Reasonable |
| 20-25 hours/week | Weaker | 3-4 hours/day | 8 weeks | Reasonable |
| 20-25 hours/week | Modest | 2-3 hours/day | 8 weeks | Reasonable |
| 25-30 hours/week | Modest | 4-5 hours/day | 6 weeks | Stretched |
| 30-35 hours/week | Modest | 5-6 hours/day | 4 weeks | Stretched |
Case 3: Working Parent Planning for Graduate Studies Needs Applied Calculus
Amelia is a parent of three children who also works full-time. Amelia has ambitious plans to return to graduate school in the next year to advance her career. Amelia cannot take a traditional classroom math course due to her schedule constraints.How fast can Amelia finish the DMAT 201 - Applied Calculus course?
We have many students like Amelia who are quite successful in Distance Calculus!
Amelia will probably do her math homework after her kids are asleep for the night, in the 10pm-midnight timeframe. The Mastery Learning format for Distance Calculus serves Amelia well, where she is able to spend extra time on those topics that are more challenging for her, without penalty or "falling behind" as she would in a traditional course.
When the children get sick and stay home from school, or life and work commands extra time, Amelia is able to take a break from Distance Calculus - usually for a few weeks, but perhaps for a few months, if needed - and return to her studies when her schedule permits. While such breaks do cause slower completion times, and "getting back in the swing of things" does require extra time and effort for Amelia, the flexibility of the asynchronous course format allows Amelia to finish the course when she can.
Case 4: 18-22 Year Old Student With Full Course Load Needs To Finish Applied Calculus
James is an undergraduate student at a university, carrying 15 semester credits - a full course load. James wants to add the Applied Calculus course to his course schedule, in order to complete a general education requirement.What are the challenges that James will face with this plan?
In our experience, when a student is faced with "too many courses" at the same time, it is the asynchronous distance course that almost always is the course to suffer a lack of attention. With other synchronous course deadlines and examinations, it is natural that an asynchronous course such as Distance Calculus becomes the "pressure valve".
Students in these situations nearly always finish their Distance Calculus course during the winter break (December, January), spring vacation (April), and/or the summer vacation months (May-August). Even with the best of intensions, it is very difficult to complete a Distance Calculus course while taking 4 or 5 other courses simultaneously.
Younger students also have more difficulty with the flexible schedule of Distance Calculus. It is very easy to put off your course work "until all day Saturday" or "next week after my Philosophy exam", which snowballs into a huge amount of work leftover to an increasingly short amount of time. Planning for vacation times is the best approach for students in this category.
Applied Calculus Referenced Colleges/Universities
Over the past 27 years, Distance Calculus has enrolled thousands of students who successfully complete the Applied Calculus courses, and use this course record towards undergraduate and graduate programs at various colleges and universities in the U.S. and throughout the world.
Below is a list of schools that Distance Calculus students have utilized their Applied Calculus course credits earned towards these programs:
- University of Pennsylvania, Wharton School of Business
- London School of Economics
- Harvard University: Kennedy School of Government, Medical Schools
- Duke University, Fuqua School of Business, Law School, Graduate Programs
- Columbia University School of Business
- University of Pennsylvania Architectural School
- University of Michigan: MBA, Medical Schools, Graduate Programs
- Stanford University, MBA
- University of California, Berkeley
- Auburn University MBA Program
- University of North Carolina, MBA
- George Washington University School of Business
- Roger Williams University
- University of Minnesota, School of Public Health
- Montclair University
- Baylor University
- Eastern Illinois University
- University of Minnesota, Twin Cities
- University of Memphis
- State University at Buffalo, Law School
- Westminster College
- University of Mississippi
- Georgia Tech
- Wharton School of Business, University of Pennsylvania
- Harvard University, Kennedy School of Government
- Duke University - Fuqua School of Business
- Stanford University
- Princeton University
- University of California, Berkeley
- University of California, Santa Barbara
- University of Southern California
- Pennsylvania State University
- College of William & Mary
- University of Texas at Austin
- Drexel University
- University of Massachusetts
- Cornell University
- University of Wisconsin, Madison
- Carnegie Mellon University
- University of North Carolina, Chapel Hill
- Kings College, University of London
- Indiana University
- Rice University
- University of Georgia
- University of South Carolina
- University of Minnesota-Twin Cities
- Baylor University
- Loma Linda University
- University of Maryland
- Georgetown University
- University of West Florida
- Eastern Illinois University
- University of Virginia
- University of Maryland
- University of Nebraska
- University of Missouri
- University of Georgia
- Florida Atlantic University
- Washington State University
- University of New Orleans
- California State University, Sacramento
- California State University, Dominguez Hills
- Babson College
- Wheaton College
- Middlebury College
- George Washington University
- Roger Williams University
- Texas A&M University
- Oregon State University
- Illinois Institute of Technology
- Montclair University
- Hillsdale University
- Evangel University
- The Art Institute of Atlanta
- New Mexico Military Institute
- Athens State University
- American Graduate University
- Kaplan University
- University of Warwick
- Gordon College
- University of Memphis
- Endicott College
- University Of Mount Union
- Mesa State College
- Azusa Pacific University
- Thomas Edison State College
- State University at Buffalo Law School
- Murray State University
- University of Phoenix
- Webster University
- Northern Michigan University
- Western Michigan University
- Central Michigan University
- Fairleigh Dickenson University
- Whitman College
- Fairifield University
- Jacksonville State University
- University of Redlands
- Westminster College
- University of San Francisco
- Strayer University
- Vanderbilt University
- Howard University
- Middlebury College
- Valdosta State University
- American University
- Clarkson University
- Howard University
- Green Mountain College
- Whittier College
- Florida A & M University
- James Madison University
- Franklin University
- Woodbury University
- Quinnipiac University
- Webster University
- Western Michigan University
Applied Calculus: Academics
80% Computer Algebra, 20% Pencil/Paper, 0% Multiple Choice
Through the usage of a computer algebra system like LiveMath™ - you will never miss a minus sign again!
Although the driving of a computer algebra system requires some up-front time to learn and master, once completed (rather quickly for most students), the time saved from having to be a "minus sign accountant" adds to the productivity of your study time. If you have ever spent hours looking for that "little numerical error", you know what we mean.
Command of a computer algebra software system is a modern-day necessity of mathematical academics. It is important, however, to retain a meaningful command of paper/pen/pencil manual computations as well. Our blend of curriculum strives for an 80%/20% split between computer algebra usage and manual computation and written skills. With each module in our curriculum, a concluding Literacy Sheet assignment ensures that each student has written mathematical competency in the subject area.
The proctored final exam is a written exam away from the computer. It is these Literacy Sheet assignments, and the continuing bridge from modern computer algebra software back to classical, manual mathematics that prepares the student from this written final exam.
We do not have any multiple-choice work. We are a real collegiate-level course program - not a "canned" set of multiple-choice question sheets which are common from large publishers and degree-mill schools.
Applied Calculus Example Curriculum
Videotext - A Modern Replacement of the Textbook
What is a videotext? It is like a textbook, except instead of being based upon printed information, this "text" is based upon video presentations as the core method of explaining the course topics. Instead of a huge, thick 1000-page Calculus textbook to lug around in your backpack, all of this new "videotext" can be loaded into your iPods or iPhones (and soon, the iPad!).Example Videos are in MP4/H.264 format, which play in most modern browsers without additional software. When additional software is required, a backup Flash player will play the video. As a backup to Flash, you may also use iTunes and/or VLC.
Our videotext features two main types of videos:
- Screencast Videos using LiveMath™ Play Video
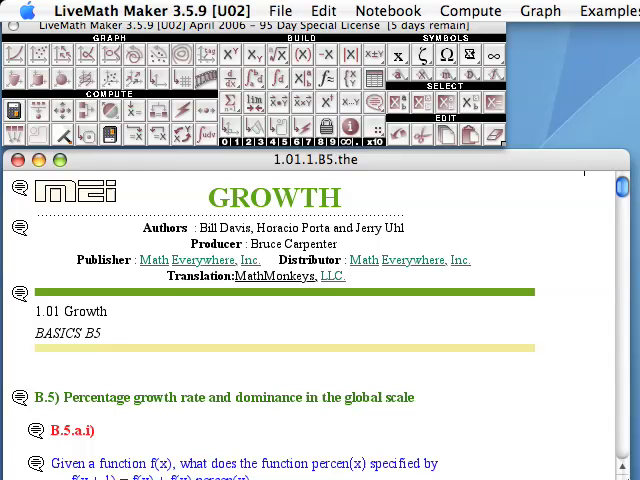
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
- ChalkTalk Videos: Manual Calculations Play Video
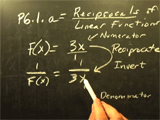
While using a computer algebra software package is a very cool way to do Calculus computations and investigations, we must also pay attention to the classical side of Calculus, and the computations that can be completed by hand with paper/pen/pencil. To be a well-rounded Calculus student, you need to be able to do calculations in both technical and manual methods.
Applied Calculus Screencast Video Questions
One extremely powerful aspect of the Distance Calculus course technologies is the usage of screencast video (and audio) recordings made by the students and the instructors, exchanged just as easily as emails back and forth.
If a picture is worth a thousand words, then a screencast movie is worth a million words - and saves boatloads of time and effort.
Instead of trying to type out a math question about a particular topic or homework question, the ease of "turning on the screen recorder" and talking and showing your question - in the span of a few minutes - can save hours of time trying to convert your question into a typed (and coherent) narrative question.
Example Instructor Question/Answer Movie
When a student asks a question in a homework notebook, sometimes the best way to explain the answer is via a screen movie.
- Instructor Question/Answer Movie Play Video
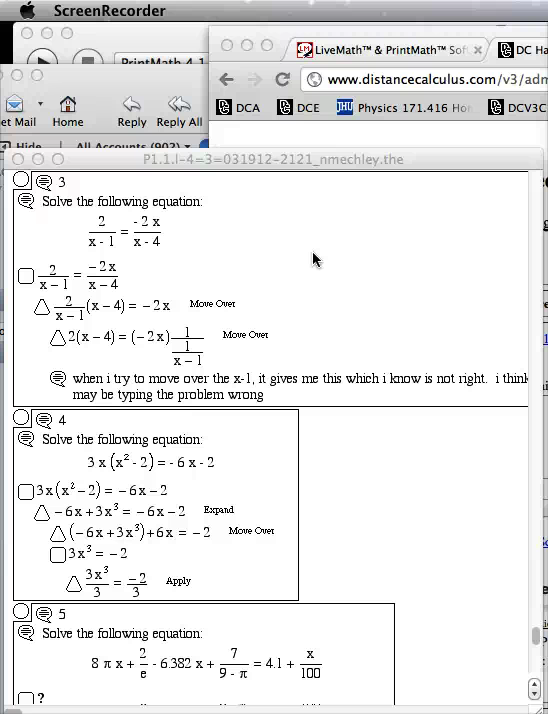
- Instructor Question/Answer Movie Play Video
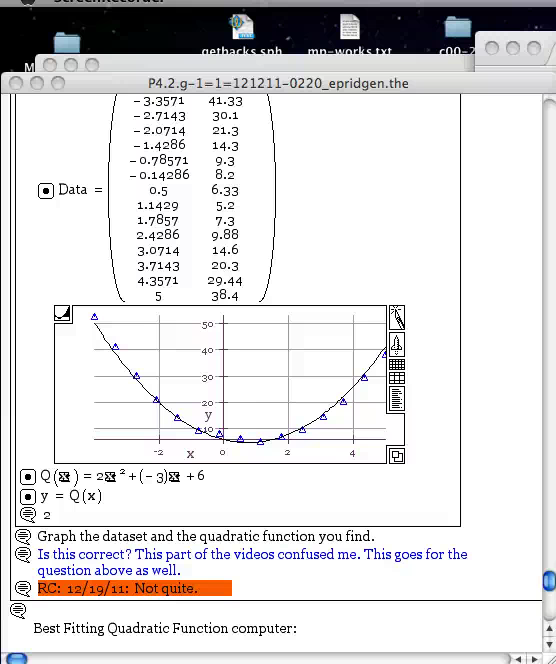
- Instructor Question/Answer Movie Play Video
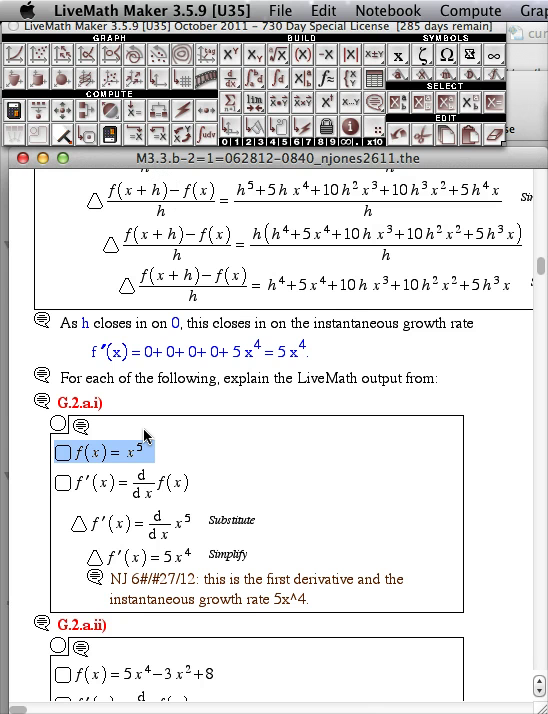
- Instructor Question/Answer Movie Play Video

- Instructor Question/Answer Movie Play Video
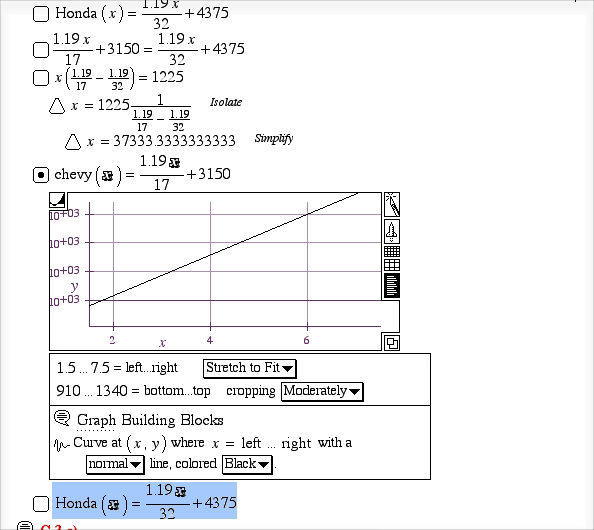
- Instructor Question/Answer Movie Play Video

Applied Calculus Example Student Work and Grading
The majority of course work occurs via the exchange of LiveMath™ notebooks - think Word Processing Files, but for mathematical computations instead of just text.
The student will "Hand-In" a notebook, and one of the instructors will grade, correct, give feedback, and/or give hints on the work in the notebook, and return the notebook to the student in his/her "GetBack" folder, where the student will view the instructor comments.
Sometimes the notebook is deemed "Complete" on the first revision. Sometimes the notebook must go back and forth between the student and instructor a number of times - 2, 3, 4, 5 times is rather common.
Coupled with the screencast video mechanism, sometimes the instructor or the student will submit a screen movie with the notebook, giving further explanation or questions in audio/video format.
Below are some example notebooks from actual students, showing the progression from starting notebook to completed notebook.
- LiveMath™ Homework Notebook #1 PDF Printout
View PDF #1
View PDF #2
View PDF #3
- LiveMath™ Homework Notebook #2 PDF Printout View PDF

- LiveMath™ Homework Notebook #3 PDF Printout View PDF

- LiveMath™ Homework Notebook #4 PDF Printout View PDF

Distance Calculus - Student Reviews





Date Posted: Apr 10, 2020
Review by: Benjamin T.
Courses Completed: Calculus I
Review: This course provided an excellent chance to learn about Calculus...again. I took calculus in high school, but I learned so much more with this course! It does take a good amount of time to do all the lessons, so definitely keep on top of them, but all the exercises helped me to really understand the material. And the nice thing is you can do it on your own time at home.
Transferred Credits to: Western University of Health Sciences: College of Optometry





Date Posted: Jan 13, 2020
Review by: Joe
Courses Completed: Calculus II
Review: This is the most interactive and productive online course I have ever taken. I had taken calculus before but never understood some of the underlying concepts until I took this course. If you want to really learn calculus in a way that will stay with you for the rest of your life, take this course.
Transferred Credits to: The college of New Jersey





Date Posted: Dec 20, 2019
Review by: Bill K.
Courses Completed: Calculus I, Calculus II, Multivariable Calculus, Linear Algebra
Review: I took the whole calculus series and Linear Algebra via Distance Calculus. Dr. Curtis spent countless hours messaging back and forth with me, answering every question, no matter how trivial they might seem. Dr. Curtis is extremely responsive, especially if the student is curious and is willing to work hard. I don't think I ever waited much more than a day for Dr. Curtis to get a notebook back to me. Dr. Curtis would also make videos of concepts if I was really lost. The course materials are fantastic. If you are a student sitting on the fence, trying to decide between a normal classroom class or Distance Calculus classes with Livemath and Mathematica, my choice would be the Distance Calculus classes every time. The Distance Calculus classes are more engaging. The visual aspects of the class notebooks are awesome. You get the hand calculation skills you need. The best summary I can give is to say, given the opportunity, I would put my own son's math education in Dr. Curtis's hands.
Transferred Credits to: None
Frequently Asked Questions
Yes, Applied Calculus, Business Calculus, Survey of Calculus - all are different names for the same level of "lower calculus", in the sense of being lower than the Engineering Calculus I course.
Yes, Applied Calculus is certainly easier than the Engineering Calculus I course, although the topics look similar when you look at a syllabus of both courses.
Yes, All Distance Calculus courses are offered through Roger Williams University in Providence, Rhode Island, USA, which is regionally accredited (the highest accreditation) through New England Commission of Higher Education (NECHE).
Yes, the majority of our Applied Calculus students are either enrolled or applying to an MBA program
Yes, the prerequisite for Applied Calculus is Algebra II from high school, which most university students have taken already. Trigonometry is not part of the prerequisite for Applied Calculus
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]

