Statistics Online Course for Academic Credit
Basic Statistics - DMAT 125 - Introduction to Computational Statistics - is the first (non-calculus-based) course on statistics and probability, often called "Elementary Statistics" or "Descriptive Statistics". Without using higher calculus techniques, this course studies Mean, Median, Mode, Frequency, Cumulative Distribution Functions, Introductory Probability, correlation and regress (data fitting), confidence intervals and hypothesis testing, and the Central Limit Theorem.
| Course Title: | Introduction to Computational Statistics |
| Catalog Number: | DMAT 125 |
| Credits: | 4 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for Introduction to Computational Statistics |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 125 - Introduction to Computational Statistics | |
Basic Statistics is often required for students who are seeking to satisfy a quantitative general education requirement, or looking towards an MBA or other graduate school program that requires a basic Statistics and Probability course.
Completion of DMAT 125 - Introduction to Computational Statistics earns 3 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
Introductory Videos
Introduction to Computational Statistics - DMAT 125 - Introduction
Basic Statistics is the classic course on the language and computations of data science, but without the calculus machinery found in the upper calculus-based Probability & Statistics course.
Basic Statistics introduces the study of data, measuring frequency, building cumulative distribution functions, investigating introductory Normal and Exponential distributions, studying data correlatiion, linear (and higher degree) curve fitting of data (regression), hypothesis testing and error estimation of measuring data. The wonderful (and bizarre) Central Limit Theorem is the culmination of the course - a very wild theorem that says if you take any data set S, the set S may not be normal (think bell-shaped curves), but if you takes sums of the data (not just averages!), the resulting changed data set will be normal (have bell-shaped curves).
Required for many undergraduate and graduate programs and courses of study, Introductory Statistics begins the study of data analysis used in some many majors and disciplines. This course is the classical "lower course" on Statistics, but starts the student into the now-popular study of Data Science, which is a combination of statistics and programming. (Students wishing to pursue a Data Science degree or certificate should look to the higher course on Probability Theory (calculus-based) and skip over this introductory DMAT 125 - Introduction to Computational Statistics course).
Different Approaches to Basic Statistics
The introductory Statistics courses around the U.S. usually fall into one of two main types - with Distance Calculus being a distinctly third-type!
| Paper Textbook Course | Excel/Minitab/SAS Course | LiveMath/Distance Calculus |
|---|---|---|
| FORMULA MEMORIZATION |
Black-Box Button Clicking | Experimentation To Conceptually Develop Computational Formulas |
| Significant Reading | Recipe-driven | Data Experiments & Written Analysis |
| Descriptive Statistics | Software Centered | Think Like a Data Scientist |
| Examples and Interpretations to Multiple Disciplines | Canned Data | Examination of Mathematical Data, Separate from the Source |
| Examples Use Hand Calculations | Calculations Using Built-In Functions | Computer-Calculations as a Tool To Understand Concepts |
| Overwhelmed with Notation | "Plug & Chug" | Strong Foundations in the Mathematics of Statistics |
Unlike its older sibling the Probability Theory course, the lower Basic Statistics course uses no calculus - the formulas only use algebra and the power of the software to carry out the computations in larger scale than could be accomplished by hand calculations.
DMAT 125 - Introduction to Computational Statistics course provides a thorough and comprehensive, yet not overwhelming, introduction to beginning Statistics.- Algebra II Refresher
Basic Statistics begins with some review of high school algebra by starting from scratch with solving basic equations, ranging then to functions, linear equations, polynomials, exponential and logarithmic functions - all base knowledge required for a mathematical study of basic statistics. This refresher aids students who have been away from academics for a while, as well as students with weaker mathematical backgrounds. For students with stronger math backgrounds, this refresher can be completed very quickly, and provides an excellent platform on which to learn the computer algebra software. - Working With Random Numbers
One of the main benefits of using a computer algebra system is the analysis of random numbers. You might think random numbers are nothing special to study - but it turns out these are the cornerstone of studying statistics and probability, and the usage of a computer algebra system such as LiveMath to generate random data and then analyze it is one of the big differences between this LiveMath-based Statistics course and the traditional textbook "here is some data" course. - Data Distributions
Looking at data by measuring frequencies and then building Cumulative Distributions Functions (CDF) is the first step in any data analysis. Utilizing LiveMath's random number generation and graphing capabilities, we explore this analysis to define data distributions, and then study the properties of these distributions, leading to the ever-important normal distribution. - Data Fitting
One of the key topics in any Basic Statistics course is: I have a big set of data, I graph it (somehow), and then ask: Can I put a line through this data plot? This leads to the topics of data correlation, and data-fitting, also called regression. Given a set of data, can I approximate that data by a linear, or quadratic, or cubic, or other type of function? - Central Limit Theorem
If you have taken any (meaningful!) Statistics course, you will have heard of the Central Limit Theorem. This theorem is so simple and profound, and quite mysterious why it works! We approach this CLT as mathematicians: given any data set S, this data many not be normally distributed, but any summation (including averages) of the data set will result in a normally distributed set. Wild wild stuff!! - Confidence Intervals
You see these all the time in the news: a survey of likely voters has a margin of error of 5.3%. How do they know this? Answer: confidence intervals!
Roger Williams University Course Catalog Listing: DMAT 125 - Introduction to Computational Statistics
Course: DMAT 125
Course Title: Introduction to Computational Statistics
Transcript Course Title (30 Characters Max:): Intro Comp Statistics
Course Description: A single course on the study of non-Calculus-based statistics, including descriptive statistics, probability, estimation, hypothesis testing, regression, and correlation, with emphasis on graphical and computational investigations, leading to the Central Limit Theorem. [4 Semester Credits]
Prerequisite: Successful completion of 3 years high school mathematics (C- or higher) or instructor consent.
E-Textbook: “The Primitives of Precalculus” by Robert R. Curtis, Ph.D.; “Statistics & LiveMath” by Robert R. Curtis, Ph.D., adapted from Davis/Porta/Uhl “Prob/Stat&Mathematica” courseware series
Software: LiveMath
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 125 - Introduction to Computational Statistics
DMAT 125 - Introduction to Computational Statistics - Learning Outcomes
- 1. To identify, manipulate, and understand the concept of data sampling
- 2. To graphically identify and numerically compute the variance, mean, median, mode, and other measures of descriptive statistics
- 3. To compute and plot various graphical descriptions of data, including histograms
- 4. To compute, manipulate, and understand basic concepts of probability measure
- 5. To compute, manipulate, and understand the concept of distributions
- 6. To identify, manipulate, and understand the core Normal distribution and its properties
- 7. To understand the Central Limit Theorem that averages of data samples tend to be normally distributed
- 8. To identify, manipulate, and compute confidence intervals and hypothesis testing
- 9. To identify, manipulate, and compute linear regression and goodness-of-fit testing
DMAT 125 - Introduction to Computational Statistics - Syllabus of Topics
1. Getting Started 1.1. Email and Chat 1.2. Learning About the Course 1.3. Required Hardware 1.4. Software Fundamentals 2. Simulations 2.1. Uniform Distributions 2.2. Area via Monte Carlo Method and Geometry 3. Data Analysis 3.1. Frequency 3.2. Expected Value 3.3. Cumulative Distributions 3.4. Variance 3.5. Histograms 3.6. Related formulas for Expected Values and Variance 4. Probabilities 4.1. Calculating Probability 4.2. Union and Intersection and Probability 4.3. Conditional Probability Formula 4.4. Independence 4.5. Indicator functions 4.6. Markov's Theorem 5. Normal and Exponential Distributions 5.1. Normal Distributions 5.2. Exponential Distribution 5.3. Classical Usage of Normal Distributions 5.4. Averages of Data and Normal Distributions 6. Random Variables 6.1. “Random Variables” 6.2. Discrete Random Variables 6.3. Expected Values and Variance 6.4. Mean, Median, and Mode 7. Correlations 7.1. Interpolation and Extrapolation 7.2. Linear, Exponential, Polynomial Fitting 7.3. Expected Values, Covariance, Correlation, Regression 7.4. Best Fit: Data to Algebra 8. Central Limit Theorem & Confidence 8.1. Central Limit Theorem 8.2. Sampling and Confidence Intervals 8.3. Hypothesis Testing
Legacy Course Connection
Legacy Distance Calculus Course:
DMAT 124 - Basic Statistics
In 2023, Distance Calculus introduced a new catalog of courses. The connection between the old courses and the new courses are given here:
Legacy Course Description: Emphasizes descriptive statistics, probability, estimation, hypothesis testing, regression and correlation. (3 credits)
Different Names for Basic Statistics
"Basic Statistics" is best described as the single semester lower-division non-calculus general Statistics course, which often has these names:
- Statistics
- Introductory Statistics
- Basic Statistics
- General Statistics
- Probability & Statistics (not calculus based)
It is important to note that Probability Theory is the higher track of Statistics, in comparison to the lower Basic Statistics course for (primarily) non-science majors.
If you are looking towards starting a study a Data Science, you should look towards taking the higher Probability Theory course - you do not need to take the lower non-calculus-based Basic Statistics course first.
Learning Outcomes for DMAT 125 - Introduction to Computational Statistics
- To identify, manipulate, and understand the concept of data sampling
- To graphically identify and numerically compute the variance, mean, median, mode, and other measures of descriptive statistics
- To compute and plot various graphical descriptions of data, including histograms
- To compute, manipulate, and understand basic concepts of probability measure
- To compute, manipulate, and understand the concept of distributions
- To identify, manipulate, and understand the core Normal distribution and its properties
- To understand the Central Limit Theorem that averages of data samples tend to be normally distributed
- To identify, manipulate, and compute confidence intervals and hypothesis testing
- To identify, manipulate, and compute linear regression and goodness-of-fit testing
Syllabus for DMAT 125 - Introduction to Computational Statistics
1. Getting Started 1.1. Email and Chat 1.2. Learning About the Course 1.3. Required Hardware 1.4. Software Fundamentals 2. Simulations 2.1. Uniform Distributions 2.2. Area via Monte Carlo Method and Geometry 3. Data Analysis 3.1. Frequency 3.2. Expected Value 3.3. Cumulative Distributions 3.4. Variance 3.5. Histograms 3.6. Related formulas for Expected Values and Variance 4. Probabilities 4.1. Calculating Probability 4.2. Union and Intersection and Probability 4.3. Conditional Probability Formula 4.4. Independence 4.5. Indicator functions 4.6. Markov's Theorem 5. Normal and Exponential Distributions 5.1. Normal Distributions 5.2. Exponential Distribution 5.3. Classical Usage of Normal Distributions 5.4. Averages of Data and Normal Distributions 6. Random Variables 6.1. Random Variables 6.2. Discrete Random Variables 6.3. Expected Values and Variance 6.4. Mean, Median, and Mode 7. Correlations 7.1. Interpolation and Extrapolation 7.2. Linear, Exponential, Polynomial Fitting 7.3. Expected Values, Covariance, Correlation, Regression 7.4. Best Fit: Data to Algebra 8. Central Limit Theorem & Confidence 8.1. Central Limit Theorem 8.2. Sampling and Confidence Intervals 8.3. Hypothesis Testing
Basic Statistics Requirements In Various Academic Disciplines and Programs
Academic programs that usually will accept the lower Basic Statistics course include:
- MBA & Business Schools
Many MBA & EMBA programs accept Basic Statistics to satisfy their statistics course requirement. - Pharmacy, Nursing, or Pre-Med Schools
- Architecture
- Baccelaureate General Education Requirements
- Other Graduate School Programs
- Primary/Secondary Education Teacher Certification
How Fast Can I Complete The Basic Statistics Course?
The lower DMAT 125 - Introduction to Computational Statistics course can be completed relatively quickly - it is not nearly as intense as the higher Probability Theory course - and Basic Statistics is intended for a general education audience.
If you need to complete the DMAT 125 - Introduction to Computational Statistics course on a fast track, the usual time needed to complete course is 3 weeks - with a dedicated effort of 15-25 hours of course study time per week - that's 2-4 hours per day. Many of our Distance Calculus students are under significant time constraints and need to finish their course very quickly, and we are very happy to accomodate such accelerated time schedules.
With that said, it is important to know that Distance Calculus cannot guarantee your particular completion date - this is dependent upon the quality of the work you submit, which is dependent upon your academic skills and course motivation. At Distance Calculus, we are very happy with a fast timeline for completion of a course, so long as the academic work is of the highest calibre. If you need to spend more time on this course in order to achieve your highest grade potential, we will insist you take that extra time that you need to succeed.
Distance Calculus Referenced Colleges/Universities
Over the past 27 years, Distance Calculus has enrolled thousands of students who successfully complete the Calculus I course, and use this course record towards undergraduate and graduate programs at various colleges and universities in the U.S. and throughout the world.Below is a list of schools (most recently, from just 2010-2013) that Distance Calculus - Calculus I students have listed as their Home Institution:
- Agnes Scott College
- Aiken Technical College
- Albany College of Pharmacy and Health Science
- Alma College
- American Public University
- Andrews University
- Arizona State University
- Athens State University
- Auburn University
- Augusta State University
- Austin Peay State University
- Baylor University
- Belmont University
- Beloit College
- Bentley University
- Berry College
- Bethany College
- Binghamton University
- Bloomsburg University
- Borough of Manhattan Community College
- Boston Conservatory
- Boston University
- Bryant University
- Buena Vista University
- California state University
- Carleton College
- Central Washington University
- Champlain College
- Chicago State University
- Clemson University
- Cleveland State University
- Coastal Carolina University
- College of Santa Fe
- Colorado Mesa University
- Colorado State University
- Columbia University
- Cornell Univeristy
- Covenant College
- Drexel University
- Duke University School of Law
- Duke University, Durham NC
- East Stroudsburg University
- Eastern Illinois University
- Elon University
- Embry Riddle Aeronautical University
- Excelsior College
- Ferris State University
- Florida Agricultural and Mechanical University
- Florida Atlantic University
- Florida International University
- Florida State University
- Fordham University
- Fox Valley Technical College
- Freed-Hardamen University
- Friends University
- George Mason university
- George Washington University
- Georgetown University
- Georgia State
- Griffith University
- Grinnell College
- Grove City College
- Hampshire College
- Hampton University
- Hillsdale College
- Hiram College
- Huntingdon College
- Illinois Institute for Technology
- Indiana University
- Iowa State University
- Jacksonville State University
- Jeff State Community College
- Johns Hopkins Univerisity
- Kalamazoo College
- Kennesaw State University
- Kentucky State University
- Kettering University
- Lebanon Valley College
- Lee University
- LeTourneau University
- Liberty University
- Lincoln University of Pennsylvania
- Marian University
- Mary Baldwin College
- Massachusetts Maritime Academy
- McHenry County College
- Mercer University
- Mercyhurst College
- Meredith College
- Miami University
- Michigan Technological University
- Middle Tennessee State University
- Millersville University
- Montana State University
- Montana Tech
- Naval Post Graduate School
- New York University
- Northeastern University
- Northern Arizona University
- Northern Michigan University
- Northwest Nazarene University
- Northwestern University
- Oberlin College
- Oglethorpe University
- Oklahoma Baptist University
- Old Dominion University
- Olympic College
- Orange Coast College
- Pacific Lutheran University
- Pennsylvania State University
- Pepperdine University
- Pomona College
- Randolph-Macon College
- Regent University
- Regis University
- Rhode Island School of Design
- Robert Morris University
- Rochester Institute of Technology
- Roger Williams University
- Roosevelt University
- Rutgers University
- Saint Anselm College
- Saint Joseph's University
- Salve Regina University
- Shepherd University
- Southern Methodist University
- St. Anselm College
- St. John's College
- State University of New York
- Stevens Institute of Technology
- Swarthmore College
- Texas A&M University
- The Citadel
- The New England Institute of Art
- The University of South Carolina
- Trinity University
- Tulane University
- University of Wisconsin
- University of Auckland, New Zealand
- University of California, Santa Cruz
- University of California, Los Angeles
- University of Central Texas
- University of Colorado
- University of Connecticut
- University of Dallas
- University of Florida
- University of Georgia
- University of Hawai'i-Manoa
- University of Illinois
- University of Michigan
- University of Minnesota
- University of Mississippi
- University of Missouri
- University of Nevada
- University of New Haven
- University of New Haven
- University of North Carolina
- University of Northern Iowa
- University of Oklahoma
- University of Otago
- University of Pennsylvania
- University of Pittsburgh
- University of Southern California
- University of Southern Indiana
- University of Sussex
- University of Tennessee
- University of Texas
- University of Utah
- University of West Alabama
- University of West Georgia
- University of Wisconsin
- University West Florida
- US Air Force Academy
- Utah Valley University
- Villanova University
- Virginia Military Institute
- Virginia Tech
- Washington State University
- Webster University
- West Chester University
- West Virginia University
- West Virginia Wesleyan College
- Western Kentucky University
- Western Michigan University
- Wheaton College
- Wheaton College (IL)
- William and Mary
- William Jewell College
- Wright State University
- Yale University
- Yonsei University
BASIC STATISTICS: ACADEMICS
Through the usage of a computer algebra system like LiveMath™ - you will never miss a minus sign again!
Although the driving of a computer algebra system requires some up-front time to learn and master, once completed (rather quickly for most students), the time saved from having to be a "minus sign accountant" adds to the productivity of your study time. If you have ever spent hours looking for that "little numerical error", you know what we mean.
Command of a computer algebra software system is a modern-day necessity of mathematical academics. It is important, however, to retain a meaningful command of paper/pen/pencil manual computations as well. Our blend of curriculum strives for an 80%/20% split between computer algebra usage and manual computation and written skills. With each module in our curriculum, a concluding Literacy Sheet assignment ensures that each student has written mathematical competency in the subject area.
The proctored final exam is a written exam away from the computer. It is these Literacy Sheet assignments, and the continuing bridge from modern computer algebra software back to classical, manual mathematics that prepares the student from this written final exam.
We do not have any multiple-choice work. We are a real collegiate-level course program - not a "canned" set of multiple-choice question sheets which are common from large publishers and degree-mill schools.
Basic Statistics Example Curriculum
Videotext - A Modern Replacement of the Textbook
What is a videotext? It is like a textbook, except instead of being based upon printed information, this "text" is based upon video presentations as the core method of explaining the course topics. Instead of a huge, thick 1000-page Calculus textbook to lug around in your backpack, all of this new "videotext" can be loaded into your iPods or iPhones (and soon, the iPad!).Example Videos are in MP4/H.264 format, which play in most modern browsers without additional software. When additional software is required, a backup Flash player will play the video. As a backup to Flash, you may also use iTunes and/or VLC.
Here are some samples of the videotext from the course curriculum::
- Screencast Videos using LiveMath™ Play Video
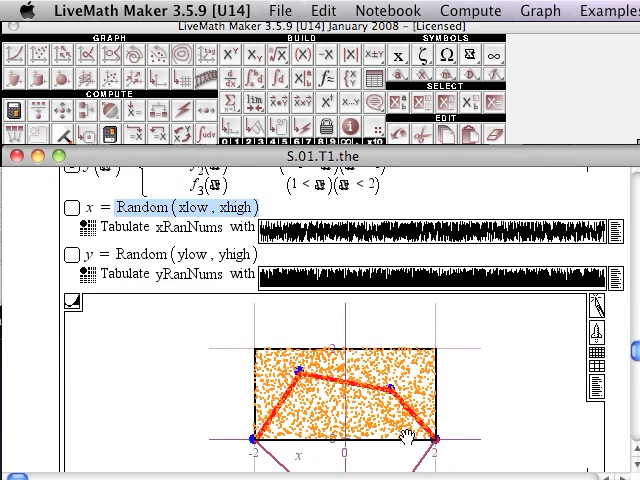
- Screencast Videos using LiveMath™ Play Video
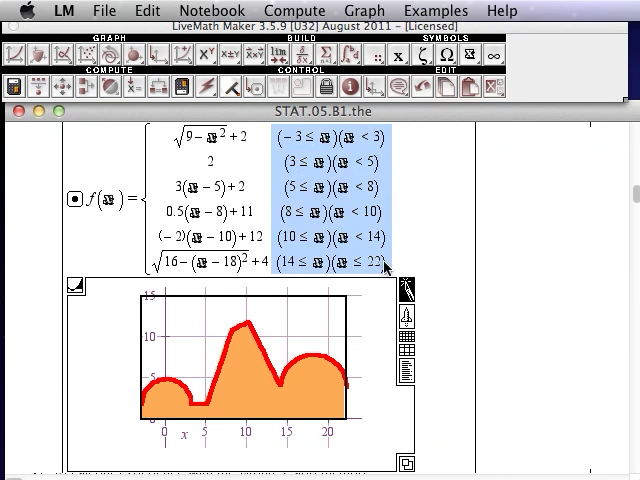
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
Basic Statistics Screencast Video Questions
One extremely powerful aspect of the Distance Calculus course technologies is the usage of screencast video (and audio) recordings made by the students and the instructors, exchanged just as easily as emails back and forth.
If a picture is worth a thousand words, then a screencast movie is worth a million words - and saves boatloads of time and effort.
Instead of trying to type out a math question about a particular topic or homework question, the ease of "turning on the screen recorder" and talking and showing your question - in the span of a few minutes - can save hours of time trying to convert your question into a typed (and coherent) narrative question.
Basic Statistics Example Student Work and Grading
The majority of course work occurs via the exchange of LiveMath™ notebooks - think Word Processing Files, but for mathematical computations instead of just text.
The student will "Hand-In" a notebook, and one of the instructors will grade, correct, give feedback, and/or give hints on the work in the notebook, and return the notebook to the student in his/her "GetBack" folder, where the student will view the instructor comments.
Sometimes the notebook is deemed "Complete" on the first revision. Sometimes the notebook must go back and forth between the student and instructor a number of times - 2, 3, 4, 5 times is rather common.
Coupled with the screencast video mechanism, sometimes the instructor or the student will submit a screen movie with the notebook, giving further explanation or questions in audio/video format.
Below are some example notebooks from actual students, showing the progression from starting notebook to completed notebook.
- LiveMath™ Example Notebook PDF Printout: Simulations: Monte Carlo Method
- LiveMath™ Example Notebook PDF Printout: Data Analysis: Frequency Plots
- LiveMath™ Example Notebook PDF Printout: Normal Distributions
Distance Calculus - Student Reviews





Date Posted: Aug 23, 2020
Review by: Sean Metzger
Student Email: seanmetzger78@gmail.com
Courses Completed: Differential Equations
Review: A lifesaver. When I found out I needed a course done in the last weeks of summer I thought there was no way i'd find one available, but this let me complete the course as quickly as I needed to while still mastering the topics. Professor always got back to me very quickly and got my assignments back to me the next day or day of. Can't recommend this course enough for students in a hurry or who just want to learn at their own pace.
Transferred Credits to: Missouri University of Science and Technology





Date Posted: Sep 20, 2020
Review by: Genevieve P.
Courses Completed: Applied Calculus
Review: I found out from my grad school after being accepted that I needed a Calculus course before starting their MBA program. I had less than 6 weeks to do it (and as a non-STEM undergrad no less). The video lectures were informative, the pre-calc refresher was great to get re-conditioned, and the asynchronous format worked so well as I did this at night/weekends after work. I completed it in 4 weeks. Professor Curtis was extremely responsive, graded assignments quickly, and a supportive guide providing constructive feedback to me to excel at the assignments. I highly recommend this course for those who need a pre-req in a hurry or like learning on their own schedule. Thanks, Distance Calculus and Professor Curtis!
Transferred Credits to: Massachusetts Institute of Technology (MIT)





Date Posted: Aug 23, 2020
Review by: Sean Metzger
Student Email: seanmetzger78@gmail.com
Courses Completed: Differential Equations
Review: A lifesaver. When I found out I needed a course done in the last weeks of summer I thought there was no way i'd find one available, but this let me complete the course as quickly as I needed to while still mastering the topics. Professor always got back to me very quickly and got my assignments back to me the next day or day of. Can't recommend this course enough for students in a hurry or who just want to learn at their own pace.
Transferred Credits to: Missouri University of Science and Technology
Frequently Asked Questions
No, not really. The student is expected to have "High School Algebra" but nearly all U.S. college/university students have taken High School Algebra, probably Algebra II, as that is a universal requirement for college/university. We do start at the very beginning, and assume that even though you have taken High School Algebra, you may not remember much of it.
No, not in the lower Statistics course. For a Calculus-based investigation of the introductory topics of statistics, check out the Probability Theory course.
No. Precalculus is a prerequisite for the higher Calculus I STEM sequence; not for the lower Statistics, single-semester course on introductory statistics (non-calculus based).
Well not from Distance Calculus! Our Statistics course is quite progressive, exploring the topics of Statistics with a laboratory-minded approach, using graphical, algebraic, and numerical tools to have a refreshing investigation of the topics of Statistics.
Yes, All Distance Calculus courses are offered through Roger Williams University in Providence, Rhode Island, USA, which is regionally accredited (the highest accreditation) through New England Commission of Higher Education (NECHE).
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]

