Calculus III Online Course for Academic Credit
STEM Calculus III - DMAT 273 - is a SPECIAL BRIDGE COURSE in the freshman (engineering) calculus sequence (STEM: Science, Technology, Engineering, and Mathematics) which is NOT NEEDED by MOST STUDENTS.
Common Semester Sequence For Calculus
The common sequence for lower division calculus looks something like this at most colleges/universities in the U.S.:| Year | Semester | Course | Topics |
| Freshman | Fall | Calculus I |
Differentiation Beginning of Integration |
| Spring | Calculus II |
Integration Techniques Series, Sequences, Taylor's Theorem Planes, Dot Product |
|
| Sophomore | Fall |
Multivariable Calculus = "Calculus III" or "Calculus IV" |
3D Planes and Surfaces Partial Derivatives Vector Fields, Path Integrals Double & Triple Integrals Gauss, Green, Stokes, Divergence Theorem (GFTOC) |
| Spring |
Differential Equations Linear Algebra |
Ordinary Differential Equations Matrix Algebra, Vector Spaces, Eigenvalues/vectors |
Some U.S. Colleges/Universites are on the QUARTER System instead of the Semester System, additionally split their lower division Calculus sequence like this:
| Year | QUARTER | Course | Topics |
| Freshman | Fall | Calculus I | Differentiation |
| Winter | Calculus II | Integration | |
| Spring | Calculus III |
Series, Sequences, Taylor's Theorem Planes, Dot Product Partial Derivatives |
|
| Sophomore | Fall |
Multivariable Calculus = "Calculus IV" |
3D Planes and Surfaces Partial Derivatives Vector Fields, Path Integrals Double & Triple Integrals Gauss, Green, Stokes, Divergence Theorem (GFTOC) |
| Winter | Differential Equations | Ordinary Differential Equations | |
| Spring | Linear Algebra | Matrix Algebra, Vector Spaces, Eigenvalues/vectors |
Special Bridge Course: DMAT 273 - Calculus III
For those students who are attempting to articulate to a Quarter-like Calculus sequence, we offer the Special Bridge Calculus III course, which, topic-wise, is 50% of our DMAT 263 - Calculus II course + 20% of our DMAT 355 - Multivariable Calculus course.
WARNING: If you are taking our standard Freshman and Sophomore Calculus sequence, you DO NOT NEED to take this DMAT 273 - Calculus III special bridge course.
will be screened to assure they are taking this extra course due to articulation needs at their college/university.
Completion of DMAT 273 - STEM Calculus II earns 3 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
| Course Title: | STEM Calculus III |
| Catalog Number: | DMAT 273 |
| Credits: | 3 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for STEM Calculus III |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 273 - STEM Calculus III | |
STEM Calculus III Introductory Videos
STEM Calculus III Course Introduction
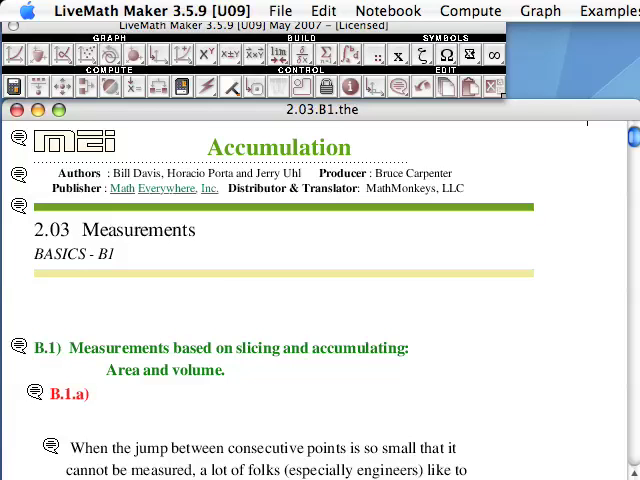
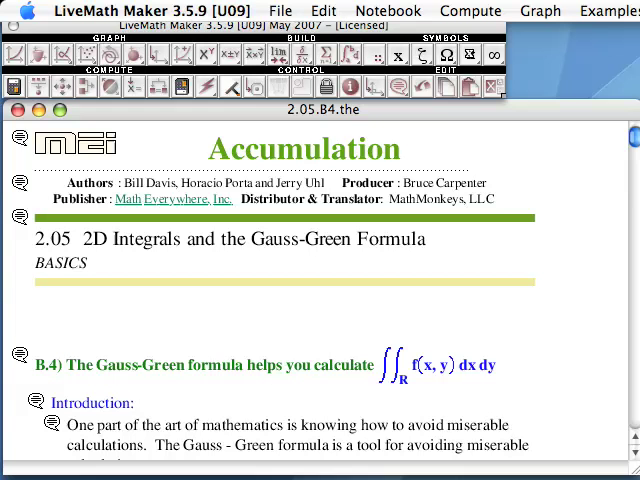
The third quarter/semester of 1st year Calculus is the preparatory course for all of the 2nd year courses (Multivariable Calculus, Differential Equations, Linear Algebra). Often referred to as "the last course on single-variable differential and integral calculus", STEM Calculus III contains the topics from the last half of our DMAT 263 - Calculus II course on sequences, series, Taylor's Theorem - via Splines - and first portion of the DMAT 355 - Multivariable Calculus & Vector Analysis.
STEM Calculus III is comprised of two distinct parts:
- Taylor's Theorem
The general concept of approximating functions using infinite polynomials, which requires the discussion on sequences, series, convergence, divergence, and error analysis. - Introduction to Multivariable Calculus
A selection of topics from the Multivariable Calculus course, specially about planes, dot products, and partial derivatives, with these topics having very little to do with the Taylor's Theorem portion of the course, but added only because of historical and articulation needs. These topics are usually the last few chapters in the big, thick first year Calculus course textbook.
Roger Williams University Course Catalog Listing: DMAT 273 - STEM Calculus III
Course: DMAT 273
Course Title: STEM Calculus III
Transcript Course Title (30 Characters Max:): STEM Calculus III
Course Description: A third course in the differential and integral calculus for engineering and science with emphasis on computational techniques, graphical analysis, and algebraic methods. Topics include splines, barriers, Taylor's Theorem, L'Hopital's Rule, infinite sequences and series, selected topics from three dimensional calculus and geometry. [3 Semester Credits]
Prerequisite: Successful completion (C- or higher) of Calculus II or equivalent, or consent of instructor.
E-Textbook: Calculus & LiveMath by Robert R. Curtis, Ph.D., adapted from Davis/Porta/Uhl Calculus&Mathematica courseware series
Software: LiveMath
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 273 - STEM Calculus III
DMAT 273 - STEM Calculus III - Learning Outcomes
- 1. To understand and compute parametric and Polar function integrals
- 2. To understand and compute splines and polynomial approximations
- 3. To understand and compute with Taylor's Theorem
- 4. To understand and compute with L'Hopital's Rule and using expansions to compute limits
- 5. To understand and compute sequences and series
- 6. To understand and compute convergence or divergence of sequences and series
- 7. To understand and compute 3D vector analysis, dot product, planes, and cross products
- 8. To understand and compute partial derivatives and tangent planes to a surface
DMAT 273 - STEM Calculus III - Syllabus of Topics
1. Getting Started 1.1. Email and Chat 1.2. Learning About the Course 1.3. Required Hardware 1.4. Software Fundamentals 2. Taylor's Expansion of a Function 2.1 Splines and Smooth Splines 2.2 Points of Contact 2.3 Application: Landing an Airplane 2.4 Taylor Expansion 2.5 Recognizing Familiar Expansions 2.6 Using Expansions for Approximations 2.7 Derivatives and Integrals of Expansions 2.8 Expansions At Other Points 2.9 Newton's Method 2.10 Calculating Limits: L'Hopital's Rule 3. Sequences and Series 3.1 Sequences of Numbers 3.2 Series of Numbers 3.3 Convergence 3.4 Convergence of Taylor Expansions 3.5 Barriers: Radius of Convergence 3.6 Shared Convergence Intervals for Derivatives and Integrals of Functions 3.7 Applications: Drug Dosing 4. Power Series 4.1 Basic Definition 4.2 Convergence Intervals of Power Series 4.3 Ratio Test and Other Convergence Tests 4.4 Finding Series Convergence Values via Power and Taylor Series 5. Polar Coordinates 5.1 Basic Graphing 5.2 Recognizable Curves 5.3 Differentiation and Integration in Polar Coordinates 6. Vector Analysis 6.1 Vector Arithmetic 6.2 Dot Product, Cross Product 6.3 Planes 6.4 Partial Derivatives 6.5 Tangent Planes
Calculus III - Example Curriculum
Videotext - A Modern Replacement of the Textbook
What is a videotext? It is like a textbook, except instead of being based upon printed information, this "text" is based upon video presentations as the core method of explaining the course topics. Instead of a huge, thick 1000-page Calculus textbook to lug around in your backpack, all of this new "videotext" can be loaded into your iPods or iPhones (and soon, the iPad!).Example Videos are in MP4/H.264 format, which play in most modern browsers without additional software. When additional software is required, a backup Flash player will play the video. As a backup to Flash, you may also use iTunes and/or VLC.
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
Calculus III - Screencast Video Questions
One extremely powerful aspect of the Distance Calculus course technologies is the usage of screencast video (and audio) recordings made by the students and the instructors, exchanged just as easily as emails back and forth.
If a picture is worth a thousand words, then a screencast movie is worth a million words - and saves boatloads of time and effort.
Instead of trying to type out a math question about a particular topic or homework question, the ease of "turning on the screen recorder" and talking and showing your question - in the span of a few minutes - can save hours of time trying to convert your question into a typed (and coherent) narrative question.
Example Student/Instructor Question/Answer Movies
When a student asks a question in a homework notebook, sometimes the best way to explain the answer is via a screen movie. We utilize easy-to-use software to create screen movies with audio so that you can communicate with your instructor "as if they were sitting at the computer with you". Students don't ask questions like this everytime they have a question, but it is a good way to ask questions after text chats aren't working.If a picture is worth a thousand words, and a movie is worth a thousand pictures, then a movie with audio is worth 1000*1000*1000 = 1,000,000,000 (billion) words!
- Student Question Movie Play Video
This screen video was created by a student in the Calculus II course, asking a question about a particular homework problem.
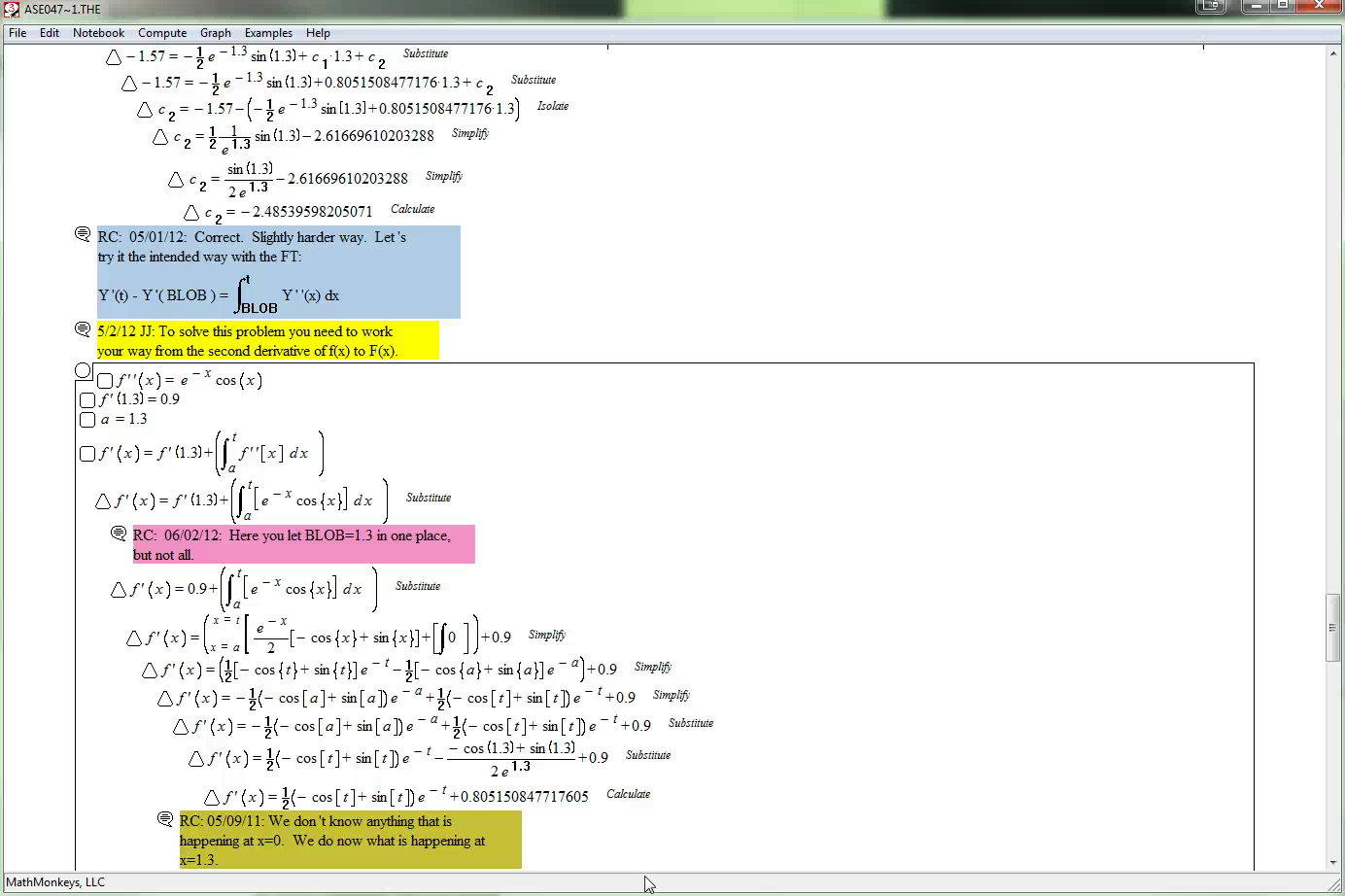
- Instructor Question/Answer Movie Play Video
This screen video was created by the instructor, answering the student's video question.
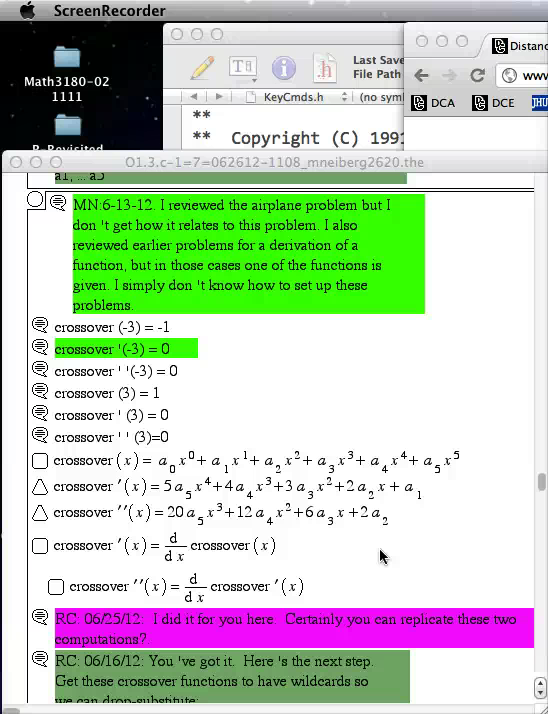
- Student Question Movie Play Video
This screen video was created by a student in the Calculus II course, asking a question about a particular homework problem.
Calculus III - Example Student Work and Grading
The majority of course work occurs via the exchange of LiveMath™ notebooks - think Word Processing Files, but for mathematical computations instead of just text.
The student will "Hand-In" a notebook, and one of the instructors will grade, correct, give feedback, and/or give hints on the work in the notebook, and return the notebook to the student in his/her "GetBack" folder, where the student will view the instructor comments.
Sometimes the notebook is deemed "Complete" on the first revision. Sometimes the notebook must go back and forth between the student and instructor a number of times - 2, 3, 4, 5 times is rather common.
Coupled with the screencast video mechanism, sometimes the instructor or the student will submit a screen movie with the notebook, giving further explanation or questions in audio/video format.
Below are some example notebooks from actual students, showing the progression from starting notebook to completed notebook.
- LiveMath™ Homework Notebook #1 PDF Printout View PDF

- LiveMath™ Homework Notebook #2 PDF Printout View PDF

Distance Calculus - Student Reviews





Date Posted: Jan 8, 2021
Review by: Cristian Mojica
Student Email: comojica@ucdavis.edu
Courses Completed: Probability Theory
Review: A fantastic course! I was able to complete it in about half a year (with a few gaps) alongside other coursework I was completing. There are no deadlines except the one-year mark after registering, so you work at your own rate and schedule. Probability Theory is required for me to apply to Master's programs in Statistics, so I was glad when I found Distance Calculus. While the course was slightly less difficult than I originally expected, there were parts that definitely slowed me down and made me think. (Also, although calculus is not everywhere in the course, it is everywhere in normal and exponential variables and beyond, so make sure to review derivatives and integrals (single and double)!) I used Mathematica for my software, and it helped speed along calculations and proved to be the perfect stage and tool for this material. I think visual learners will absolutely revel in how the material is presented in this course. (I know I did!) As there is plenty of writing and calculation to do, you have many opportunities to develop and strengthen your voice as a mathematician. The modern format of 80% electronic notebook work and 20% handwritten work is an excellent mixture for studying probability theory and grasping its core ideas. Dr. Curtis is clear in his answers to any questions and concerns you may have and is highly responsive to email and chat, and to responses you leave in your notebooks. He truly wants to help you and to see you succeed, and he is always on your side. I highly recommend Probability Theory with Distance Calculus!




Date Posted: Feb 28, 2020
Review by: Teddy M.
Courses Completed: Precalculus, Calculus I
Review: Pros: once you get going, you can go really fast. The visual textbook is pretty cool. The instructors were very responsive. Cons: the movies are great, but the software crashes more than it should. Sometimes it is just a hassle doing things in the software instead of on paper, but once I got used to the software, it was ok.
Transferred Credits to: Texas Christian University





Date Posted: May 3, 2018
Review by: James Holland
Courses Completed: Calculus I, Calculus II
Review: I needed to finish the Business Calculus course very very very fast before my MBA degree at Wharton started. With the AWESOME help of Diane, I finished the course in about 3 weeks, allowing me to start Wharton on time. Thanks Diane!
Transferred Credits to: Wharton School of Business, University of Pennsylvania
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]