Calculus I Online Course for Academic Credit
Calculus I (Calculus 1) is the first course in the freshman (engineering) calculus (STEM: Science, Technology, Engineering, and Mathematics) sequence as a comprehensive introduction to the mathematical concepts of differentiation and integration, culminating with the Fundamental Theorem of Calculus.
| Course Title: | STEM Calculus I |
| Catalog Number: | DMAT 253 |
| Credits: | 4 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for STEM Calculus I |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 253 - STEM Calculus I | |
Completion of DMAT 253 - STEM Calculus I earns 4 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
Introductory Videos
STEM Calculus I - DMAT 253 - Introduction
Calculus I is the gateway to collegiate mathematics. As such, STEM Calculus I is often a prerequisite course for many majors, both science and non-science.Calculus I introduces the fundamental concept of the derivative, geometrically demonstrated in this animation showing a limit of secant lines approaching a tangent line at a point on a curve y=f(x):
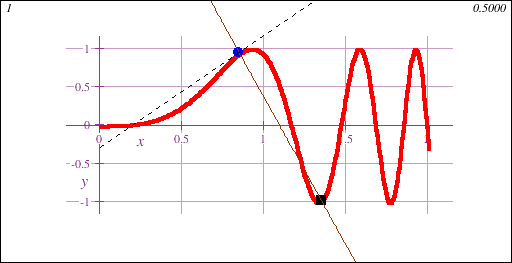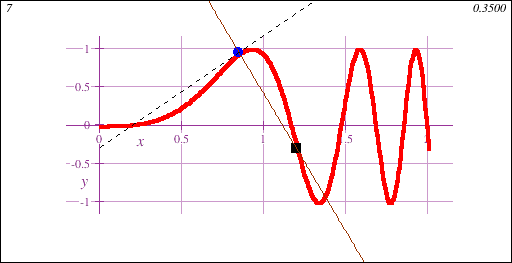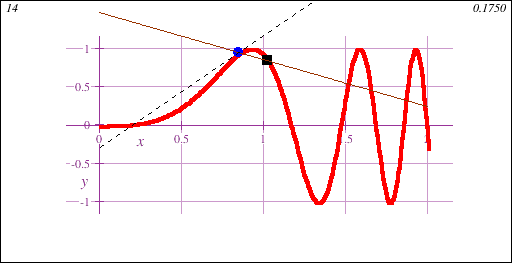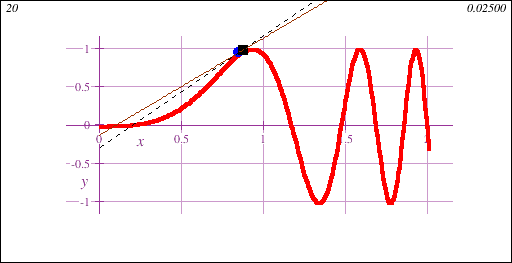
STEM Calculus I also introduces the fundamental concept of the integral, geometrically demonstrated in this animation showing the accumulation of signed area under a curve y=f(x) of increasing accuracy:
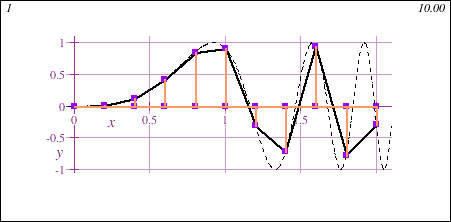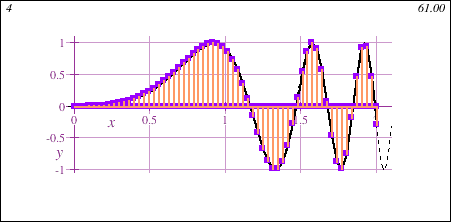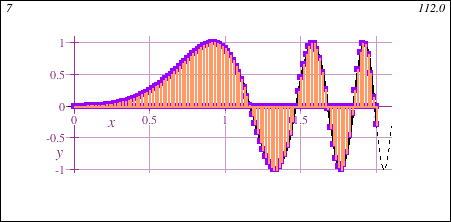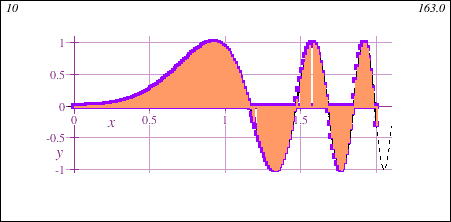
- Intensive Precalculus Refresher
STEM Calculus I starts with an intensive 26 assignment refresher of precalculus including trigonometric functions, starting from scratch with solving basic equations, ranging then to functions, linear equations, polynomials, exponential, logarithmic, and trigonometric functions. This refresher aids students who have been away from academics for a while, as well as students with weaker mathematical backgrounds. For students with stronger math backgrounds, this refresher can be completed very quickly, and provides an excellent platform on which to learn the computer algebra software. - Analytic Geometry
STEM Calculus I usually includes an exploration of conic sections: parabola, hyperbola, ellipse. These topics are included for transferability requirements, as many schools in the U.S. still require these topics to be included in the Calculus I course, although many Precalculus courses are charged with presentation of these topics. - Introduction to Differential Calculus
STEM Calculus I begins with investigating the phenomena of growth of the various types of functions, culminating with the derivative as a measurement of growth. Limits of functions and their usage in formulating the algebraic rules for computing derivatives - Newton's "calculus" - are examined both in classical algebraic terms, and numerically and graphically with modern computer algebra and graphing tools. Applications of the derivative to "max/min" problems, differential equations, related rates, implicit differentiation, sum/product/chain rules, rates of change, and parametric equations are then studied. - Introduction to Integral Calculus
STEM Calculus I studies the connection between integrals as measurement of signed area of regions defined by function curves, exploring the algebraic, graphical, and numerical aspects of integrals, in connection with introductory differential equations. Algebraic methods for computing basic integrals, followed by the introduction of the Fundamental Theorem of Calculus, along with the intial methods for computing integrals algebraically are then studied.
Roger Williams University Course Catalog Listing: DMAT 253 - STEM Calculus I
Course: DMAT 253
Course Title: STEM Calculus I
Transcript Course Title (30 Characters Max:): STEM Calculus I
Course Description: A first course introduction to differential and integral calculus for engineering and science students, with emphasis on a modern, empirical exposition of the classical subject. Topics include a study of the algebraic, numerical, and graphical aspects of polynomial, exponential, logarithmic, and trigonometric functions, limits, function growth, derivative analysis and optimization, introduction to differential equations, methods and applications of integration, and the Fundamental Theorem of Calculus. [4 Semester Credits]
Prerequisite: Successful completion (C- or higher) of Precalculus with Trigonometry or equivalent, or consent of instructor.
E-Textbook: “The Primitives of Precalculus” by Robert R. Curtis, Ph.D.; “Calculus & LiveMath” by Robert R. Curtis, Ph.D., adapted from Davis/Porta/Uhl “Calculus&Mathematica” courseware series.
Software: LiveMath
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 253 - STEM Calculus I
DMAT 253 - STEM Calculus I - Learning Outcomes
- 1. To identify, manipulate, and understand the algebraic, numerical, and graphical fundamentals of linear, polynomial, exponential, logarithmic, rational polynomial, and trigonometric functions;
- 2. To understand and compute algebraic, numerical, and graphical limits at finite and infinite values;
- 3. To understand and compute the fundamental concept of the derivative;
- 4. To understand and compute various measurements of growth of a function
- 5. To algebraically compute derivatives of common functions using summation, product, quotient, and chain rules for derivatives;
- 6. To understand and compute optimization of functions using derivatives, finding critical values;
- 7. To understand and compute the second derivative;
- 8. To understand and compute the Mean Value Theorem and related concepts;
- 9. To understand and compute first order differential equations;
- 10. To understand and compute implicit differentiation and related rates;
- 11. To understand and compute parametric equations, including projectile motion;
- 12. To understand and calculate numerically and graphically the core concepts of the integral for applications to signed area measurements;
- 13. To compute numerically, algebraically, and graphically integrals of a variety of functions;
- 14. To algebraically compute integrals of basic polynomial, exponential, and trigonometric functions, with an introduction to the algebraic substitution technique;
- 15. To use the tools of differential and integral calculus in various applications
- 16. To understand and compute the Fundamental Theorem of Calculus
- 17. To understand and compute an integral functions, including inverse trigonometric and logarithmic integrals that do not algebraically resolve;
- 18. To utilize computer algebra and graphing software to amplify traditional manual computation techniques.
DMAT 253 - STEM Calculus I - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. The Big Picture 2.1 Solving (easy) equations in 1 variable. 2.2 What if you can't solve for x? 2.3 Finding solutions numerically 2.4 Finding solutions graphically 2.5 Solving equations of more than 1 variable 3. Functions 3.1 Function notation. 3.2 Data sets 3.3 Graphing functions 3.4 Data sets and smooth curves 3.5 Domain and Range 3.6 Algebraic combinations of functions 4. Linear Functions 4.1 Algebraic definition 4.2 Slope 4.3 Graphing linear functions by hand 4.4 Properties of linear functions 4.5 Linear data sets 5. Quadratic Functions 5.1 Algebraic definition 5.2 Graphing and Properties of Quadratic Functions 5.3 Solving quadratic equations algebraically: Factoring 5.4 Solving quadratic equations algebraically: Quadratic formula 5.5 Solving quadratic equations numerically and graphically 6. Power and Polynomial Functions 6.1 Algebraic definition 6.2 Graphing and Properties of Polynomial Functions 6.3 Solving polynomial equations algebraically: factoring 6.4 Solving polynomial equations numerically and graphically 6.5 Radicals and fractional exponents 7. Rational Polynomial Functions 7.1 Algebraic definition 7.2 Graphing and Properties of Rational Polynomial Functions 7.3 Solving rational polynomial equations algebraically: factoring 8. Exponential and Logarithmic Functions 8.1 Algebraic definition 8.2 Graphing and Properties of Exponential Functions 8.3 Solving exponential equations numerically and graphically 8.4 Exponential Growth and Applications 8.5 Data sets and exponential functions 8.6 Inverse Functions 8.7 Graphing and Properties of Logarithmic Functions 8.8 Logarithmic Growth and Applications 9 Trigonometric Functions 9.1 Graphical Properties of Trigonometric Functions 9.2 Amplitude, Phase Shift, Vertical Shift, Period, Frequency 9.3 Solving Equations Involving Trigonometric Functions 9.4 Data Sets and Trigonometric Functions 10. Growth: Preparing for the Derivative 10.1 Growth of Linear Functions 10.2 Growth of Power Functions 10.3 Growth of Exponential Functions 10.4 Dominance of Growth of Functions 10.5 Percentage Growth of Functions 10.6 Global Scale: Infinite Limits 10.7 Data Functions and Interpolation 10.8 Approximation of Functions by Linear Functions 11. Continuity 11.1 Limits 11.2 Continuous Functions 11.3 Jump Discontinuities 11.4 Piecewise Functions and Continuity 11.5 Limit Rules 12. Exponential Functions and Natural Logarithms 12.1 e = Euler's Number 12.2 Natural Logarithm 12.3 Growth Analysis 12.4 Applications: Carbon Dating 12.5 Percentage Growth and Steady Growth of Exponential Functions 12.6 Data Functions and Logarithmic Analysis 12.7 Inverse Functions 12.8 Applications: Compound Growth Rates 12.9 Applications: World Population 13. The Derivative of Polynomial, Exponential, Logarithmic, and Fractional Powers 13.1 Instantaneous Growth Rates 13.2 Definition of the Derivative 13.3 Computing the Derivative Graphically 13.4 Computing the Derivative Algebraically 13.5 Computing the Derivative Numerically 13.6 Average Growth Rate vs. Instantaneous Growth Rate 13.7 Applications of the Derivative: Spread of Disease 13.8 Finding Maxima and Minima of Functions 13.9 Relating a Function and Its Derivative 14. Computing Derivatives 14.1 Sum, Difference, Product, Quotient Rule 14.2 Chain Rule 14.3 Instantaneous Percentage Growth 14.4 Growth Dominance 15. Using Derivatives 15.1 Finding Maxima and Minima 15.2 Finding Good Representative Plots 15.3 Applications: Maximizing Volume 15.4 The Second Derivative 15.5 Applications: The Space Shuttle Challenger 15.6 Parametric Curves and Projectile Motion 16. Differential Equations 16.1 Linear Differential Equations 16.2 Logistic Equations 16.3 Rate Track Principal 16.4 Approximations - Introduction to Taylor's Theorem 17. Integration 17.1 Measuring Area Under a Curve 17.2 Definition of the Integral 17.3 Properties of Integrals, Symmetry 17.4 Integrals of Data Functions 17.5 Numerical Methods: Rectangles, Trapezoids 17.6 Undefined Integrals 17.7 Numerical Calculation of Integrals 18. Fundamental Theorem of Calculus 18.1 Derivative of an Integral 18.2 Integral of a Derivative 18.3 Fundamental Formula 18.4 Distance, Velocity, and Acceleration 18.5 Improper Integrals 18.6 Properties of Integrals 18.7 Applications: Measure Accumulation Totals 18.8 Indefinite Integrals and Antiderivatives 18.9 u-Substitution 18.10 Inverse Circular and Hyperbolic Trigonometric Functions
Legacy Course Connection
Legacy Distance Calculus Course:
DMAT 213 - Calculus I with Lab
In 2023, Distance Calculus introduced a new catalog of courses. The connection between the old courses and the new courses are given here:
Legacy Course Description: Covers the differential calculus of a single variable and introduces integration. Topics include limits and continuity, differentiation of algebraic and transcendental functions, applications of derivatives to rates of change, optimization, and curve sketching, and the Fundamental Theorem. The laboratory component involves use of computer algebra software. (4 credits)
Different Names for Calculus I
"Calculus I" (Calculus 1) is best described as the first semester of the lower-division calculus sequence, which often has these names:
- Calculus I
- Analytical Geometry and Calculus I
- Calculus 1
- Engineering Calculus I
- AP Calculus AB
It is important to note that Calculus I is the higher track of Calculus, in comparison to the lower Applied Calculus track for (primarily) non-science majors.
If you are not a science major (e.g. MBA, Nursing/Pharmacy, Other Graduate), check out the Applied Calculus page for more information on that lower-level course. If your need for a "one semester course of differential and integral calculus" will be satisfied in the lower Applied Calculus course, it is best to enroll in that lower course.
Prerequisites for DMAT 253 - Calculus I
Calculus I provides an introduction to differential and integral calculus, usually in preparation for completing the Calculus II second semester of Calculus, and perhaps higher sophomore-level Calculus sequence courses (Vector/Multivariable Calculus, Differential Equations, Linear Algebra, Probability Theory).Our online Calculus 1 course for college credit has the prerequisite of College Algebra and Trigonometry, or the combined Precalculus course.
The main topical differences between the lower Applied Calculus and the higher (Engineering) Calculus I course are described in the table below.
| Topic | Applied Calculus | Calculus I |
|---|---|---|
| Trigonometry | No | Yes |
| Functions | Polynomials, Roots, Exponential, Logarithmic | Polynomials, Roots, Exponential, Logarithmic, Trigonometric, Composite, Integral Functions |
| Limits | Mainly Graphical, Numerical | Algebraic, Graphical, Numerical |
| Derivatives | Simple Algebraic Rules, Chain Rule | Rigorous Rule Development, Application, Implicit Differentiation, Chain Rule |
| Applications | Economics, Finance, Easier | Physics, Economics, Rates, Challenging, Mean Value Theorem |
| Introduction to Differential Equations | No | Yes |
| Derivatives and Integrals of Parametric Curves/Functions | No | Yes |
| Displacement, Velocity, Acceleration | Minimal | Yes |
| Integration | Basic Integration Rules, Basic Fundamental Theorem of Calculus | Algebraic Integration, Integral Functions, Integration via Substitution, Preparation for Calculus II, Fundamental Theorem of Calculus |
The Applied Calculus course does include more applications to business, finance, economics, etc. than does the Engineering Calculus 1 course.
The higher Engineering Calculus 1 course materials contain the standard course topics found in the higher Calculus I course, distinctively: trigonometric functions and exponential functions feature prominently, the Mean Value Theorem (MVT), the Fundamental Theorem of Calculus (FTOC), rates of change (implicit differentiation).
Course Syllabus for DMAT 253 - STEM Calculus I
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. The Big Picture 2.1 Solving (easy) equations in 1 variable. 2.2 What if you can't solve for x? 2.3 Finding solutions numerically 2.4 Finding solutions graphically 2.5 Solving equations of more than 1 variable 3. Functions 3.1 Function notation. 3.2 Data sets 3.3 Graphing functions 3.4 Data sets and smooth curves 3.5 Domain and Range 3.6 Algebraic combinations of functions 4. Linear Functions 4.1 Algebraic definition 4.2 Slope 4.3 Graphing linear functions by hand 4.4 Properties of linear functions 4.5 Linear data sets 5. Quadratic Functions 5.1 Algebraic definition 5.2 Graphing and Properties of Quadratic Functions 5.3 Solving quadratic equations algebraically: Factoring 5.4 Solving quadratic equations algebraically: Quadratic formula 5.5 Solving quadratic equations numerically and graphically 6. Power and Polynomial Functions 6.1 Algebraic definition 6.2 Graphing and Properties of Polynomial Functions 6.3 Solving polynomial equations algebraically: factoring 6.4 Solving polynomial equations numerically and graphically 6.5 Radicals and fractional exponents 7. Rational Polynomial Functions 7.1 Algebraic definition 7.2 Graphing and Properties of Rational Polynomial Functions 7.3 Solving rational polynomial equations algebraically: factoring 8. Exponential and Logarithmic Functions 8.1 Algebraic definition 8.2 Graphing and Properties of Exponential Functions 8.3 Solving exponential equations numerically and graphically 8.4 Exponential Growth and Applications 8.5 Data sets and exponential functions 8.6 Inverse Functions 8.7 Graphing and Properties of Logarithmic Functions 8.8 Logarithmic Growth and Applications 9. Trigonometric Functions 9.1 Graphical Properties of Trigonometric Functions 9.2 Amplitude, Phase Shift, Vertical Shift, Period, Frequency 9.3 Solving Equations Involving Trigonometric Functions 9.4 Data Sets and Trigonometric Functions 10. Growth: Preparing for the Derivative 10.1 Growth of Linear Functions 10.2 Growth of Power Functions 10.3 Growth of Exponential Functions 10.4 Dominance of Growth of Functions 10.5 Percentage Growth of Functions 10.6 Global Scale: Infinite Limits 10.7 Data Functions and Interpolation 10.8 Approximation of Functions by Linear Functions 11. Continuity 11.1 Limits 11.2 Continuous Functions 11.3 Jump Discontinuities 11.4 Piecewise Functions and Continuity 11.5 Limit Rules 12. Exponential Functions and Natural Logarithms 12.1 e = Euler's Number 12.2 Natural Logarithm 12.3 Growth Analysis 12.4 Applications: Carbon Dating 12.5 Percentage Growth and Steady Growth of Exponential Functions 12.6 Data Functions and Logarithmic Analysis 12.7 Inverse Functions 12.8 Applications: Compound Growth Rates 12.9 Applications: World Population 13. The Derivative of Polynomial, Exponential, Logarithmic, and Fractional Powers 13.1 Instantaneous Growth Rates 13.2 Definition of the Derivative 13.3 Computing the Derivative Graphically 13.4 Computing the Derivative Algebraically 13.5 Computing the Derivative Numerically 13.6 Average Growth Rate vs. Instantaneous Growth Rate 13.7 Applications of the Derivative: Spread of Disease 13.8 Finding Maxima and Minima of Functions 13.9 Relating a Function and Its Derivative 14. Computing Derivatives 14.1 Sum, Difference, Product, Quotient Rule 14.2 Chain Rule 14.3 Instantaneous Percentage Growth 14.4 Growth Dominance 15. Using Derivatives 15.1 Finding Maxima and Minima 15.2 Finding Good Representative Plots 15.3 Applications: Maximizing Volume 15.4 The Second Derivative 15.5 Applications: The Space Shuttle Challenger 15.6 Parametric Curves and Projectile Motion 16. Differential Equations 16.1 Linear Differential Equations 16.2 Logistic Equations 16.3 Rate Track Principal 16.4 Approximations - Introduction to Taylor's Theorem 17. Integration 17.1 Measuring Area Under a Curve 17.2 Definition of the Integral 17.3 Properties of Integrals, Symmetry 17.4 Integrals of Data Functions 17.5 Numerical Methods: Rectangles, Trapezoids 17.6 Undefined Integrals 17.7 Numerical Calculation of Integrals 18. Fundamental Theorem of Calculus 18.1 Derivative of an Integral 18.2 Integral of a Derivative 18.3 Fundamental Formula 18.4 Distance, Velocity, and Acceleration 18.5 Improper Integrals 18.6 Properties of Integrals 18.7 Applications: Measure Accumulation Totals 18.8 Indefinite Integrals and Antiderivatives 18.9 u-Substitution 18.10 Inverse Circular and Hyperbolic Trigonometric Functions
TYPICAL STUDENTS IN CALCULUS I - Example Student Profiles
Case 1: Returning To Graduate School
Kelly is planning to go to graduate school in Economics, and the degree program she wishes to enroll in requires her to complete Calculus I, Calculus II, and Differential Equations. Kelly took a Calculus course back in her undergraduate days, but it has been too many years to rely upon that course information to move forward in the Calculus sequence.How fast can Kelly finish the DMAT 253 - Calculus I (Calculus 1 online course) course?
Graduate school-bound students tend to be highly motivated, and they usually have a timeline they need to follow to complete these courses.
| Common Completion Timelines for DMAT 253 - Calculus I (Calculus 1 online course) | ||||
| Hours Dedicated | Math Skills | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-10 hours/week | Weaker | 1-2 hours/day | 16 weeks | Reasonable |
| 7-12 hours/week | Modest | 2-3 hours/day | 12 weeks | Reasonable |
| 10-15 hours/week | Stronger | 3-4 hours/day | 8 weeks | Reasonable |
| 15-20 hours/week | Strong | 5-6 hours/day | 6 weeks | Stretched |
| 20-25 hours/week | Strong | 5-7 hours/day | 4 weeks | Stretched |
| 25-35 hours/week | Strong | 6-8 hours/day | 3 weeks | World's Record |
Time commitments are important for success in an online Calculus I course for college credit from Distance Calculus. There are no fixed due dates in the Distance Calculus online courses, so it is important that students instead set their schedules for a dedicated amount of time towards the coursework.
It is also very important to consider that going faster through a course is DIRECTLY DEPENDENT upon your math skill level, and your successful engagement of the course. We require that you complete the course in a Mastery Learning format. If you are struggling with the course content, or trying to go too fast where the quality of your submitted work is suffering, then the instructors will force a slow-down of your progress through the course, even if you have fixed deadlines.
Case 2: Undergraduate Student Needs Calculus I
Jim is an undergraduate student at a university. Jim attempted the Calculus I course at his school, but he was not successful. He wants to take Calculus I via Distance Calculus online courses to get back on track with his major requirements.What are some issues Jim should consider?
Lack of success in a traditional course can be caused by many factors, some of which include:
- Classroom Lecture Structure
Some students are very good at the classroom lecture paradigm, some are not. 100+ students in a big lecture hall is not the best learning environment for many students. - Traditional Course Pace
In a traditional course, the student must keep pace with the rest of the class. If a student has weakness in a particular area (e.g. trigonometry), the student is expected to kick into "high gear" to make up the distance. Sometimes this re-doubling of effort is not enough to stay on pace with the lectures and the homework due dates. - Too Many Other Classes
Often traditional undergraduate students find themselves taking 5 courses concurrently. When the scheduling pressure reaches critical with exams and papers due, often one course will suffer. Ambitious scheduling for a "tough semester" will sometimes not follow the planned path. Courses that require ample amounts of time and effort - like a Calculus 1 online course - can fall by the wayside.
Adding Calculus I (Calculus 1 online course) via the Distance Calculus online courses in addition to a full-load of 4-5 other traditional courses is usually not advised.
Case 3: High School Student & AP Calculus
Alicia is an ambitious high school student. Alicia is taking a number of AP courses, but the AP Calculus course has a time conflict at her high school. Alicia plans to take Calculus I (Calculus 1 online course) via Distance Calculus instead of the AP Calculus course.What are some issues that Alicia should consider?
There are positive and negative issues to consider with such a plan. Most often, our ambitious high school students are successful in the Distance Calculus online courses, as these students are successful in all tasks they engage in.
Positive Aspects
- Collegiate Calculus I While in High School
Although the content of the AP Calculus course is at the collegiate level, most AP Calculus courses are still offered just like other high school courses. The parameters of collegiate courses - expectations of additional written work, thorough solution presentations, challenging problems and approaches to concepts - are often not found in the AP Calculus courses, which are set towards the successful completion of the AP Calculus exam. - AP Calculus Exam Not Required
As the Calculus I (Calculus 1) via Distance Calculus is a real collegiate-level, academic-credit-earning course, the AP Calculus exam is not required to earn the collegiate credit hours. Some students do not like high-stakes exams like the AP Calculus exam. This makes our online Calculus 1 course for college credit an ideal solution for these students. - Asychronous Course & High School Class Schedule
High school students have an expected 8am-3pm school day, which makes it difficult to attend a traditional college lecture course, except for night courses. As all Distance Calculus online courses are asynchronous, high school students will be able to complete the course without impacting their regular daytime class schedule.
Negative Aspects
- Lack of AP-Inflated GPA
At many high schools, AP courses award GPA points with an inflated multiplier - often 1.3. In this way, ambitious students are able to inflate their GPAs, often higher than 4.0, which is beneficial to collegiate applications. Distance Calculus courses do not offer this kind of GPA help. - Academic Immaturity
The first real collegiate course a high school student takes is often a bit shocking. High school courses tend to be very "answer-centered", while a collegiate course is usually less so, and more "open ended". In Distance Calculus, there is no "answer key" to check your answers, as many high school math courses are geared for. For these reasons, some high school students experience an unfamiliar sense of unsuccessfulness at the beginning of the course, which is disconcerting for many.
For some students, an online Calculus 1 course for college credit sounds great, but does not turn out to be a good fit for students who prefer a "plug and chug" course.
Case 4: Non-Science Major, But Applied Calculus Is Not Acceptable
Rashida is a pharmacy student, looking towards pharmacy school, which requires a "single semester introductory Calculus course." Rashida checks with her pharmacy school, and they tell her that the lower Applied Calculus course is not acceptable for their program, but the higher Calculus I (Calculus 1) course is acceptable.What are some issues Rashida should consider?
The Calculus I course is the higher, more rigorous, more challenging course when compared to the lower Applied Calculus course. But the two courses are built from the same core e-textbook, so the higher level of difficulty should be thought of as more challenging, rather than "impossible".
Rashida should consider these items:
- Precalculus & Trigonometry
The Calculus I course has a prerequisite of Precalculus with Trigonometry. Rashida remembers that she never took trigonometry in high school. That means Rashida will need to start with the Precalculus course before moving forward into the Calculus I (Calculus 1) course. - Extra Time for Calculus I
As Calculus I is more challenging than the lower Applied Calculus, Rashida will need to plan for taking a bit longer to complete the Calculus I course. The 8-12 week completion plan is probably the fastest that Rashida will be able to complete Calculus I (which does not include another 6-8 weeks to complete the Precalculus course first). - Courseload Considerations
Rashida is finishing up her undergraduate work, and has a full load of senior-level classes. Adding Calculus I to this full-load is not advisable. It may be best for Rashida to wait for her current semester to end and to take up Calculus I as her single-focus course.
Case 5: Working Parent Planning for Graduate Studies Needs Calculus I
Amelia is a parent of three children who also works full-time. Amelia has ambitious plans to return to graduate school in the next year to advance her career. Amelia cannot take a traditional classroom math course due to her schedule constraints.How fast can Amelia finish the DMAT 253 - Calculus I course?
We have many students like Amelia who are quite successful in Distance Calculus!
Amelia will probably do her math homework after her kids are asleep for the night, in the 10pm-midnight timeframe. The Mastery Learning format for the Distance Calculus online courses serve Amelia well, where she is able to spend extra time on those topics that are more challenging for her, without penalty or "falling behind" as she would in a traditional course.
When the children get sick and stay home from school, or life and work commands extra time, Amelia is able to take a break from Distance Calculus - usually for a few weeks, but perhaps for a few months, if needed - and return to her studies when her schedule permits. While such breaks do cause slower completion times, and "getting back in the swing of things" does require extra time and effort for Amelia, the flexibility of the asynchronous course format allows Amelia to finish the course when she can.
Case 6: 18-22 Year Old Student With Full Course Load Needs To Finish Calculus I
James is an undergraduate student at a university, carrying 15 semester credits - a full course load. James wants to add the Applied Calculus course to his course schedule, in order to complete a general education requirement.What are the challenges that James will face with this plan?
In our experience, when a student is faced with "too many courses" at the same time, it is the asynchronous distance course that almost always is the course to suffer a lack of attention. With other synchronous course deadlines and examinations, it is natural that an asynchronous course such as Distance Calculus becomes the "pressure valve".
Students in these situations nearly always finish their Distance Calculus online courses during the winter break (December, January), spring vacation (April), and/or the summer vacation months (May-August). Even with the best of intensions, it is very difficult to complete a Distance Calculus course while taking 4 or 5 other courses simultaneously.
Younger students also have more difficulty with the flexible schedule of Distance Calculus online courses. It is very easy to put off your course work "until all day Saturday" or "next week after my Philosophy exam", which snowballs into a huge amount of work leftover to an increasingly short amount of time. Planning for vacation times is the best approach for students in this category.
For many students, an online Calculus 1 course for college credit is a course that can fit in between other courses on regular semester schedules.
Distance Calculus Referenced Colleges/Universities
Over the past 27 years, Distance Calculus has enrolled thousands of students who successfully complete the Calculus I (Calculus 1) course, and use this course record towards undergraduate and graduate programs at various colleges and universities in the U.S. and throughout the world.Below is a list of schools that Distance Calculus - Calculus I (Calculus 1) students have listed as their Home Institution:
- Agnes Scott College
- Aiken Technical College
- Albany College of Pharmacy and Health Science
- Alma College
- American Public University
- Andrews University
- Arizona State University
- Athens State University
- Auburn University
- Augusta State University
- Austin Peay State University
- Baylor University
- Belmont University
- Beloit College
- Bentley University
- Berry College
- Bethany College
- Binghamton University
- Bloomsburg University
- Borough of Manhattan Community College
- Boston Conservatory
- Boston University
- Bryant University
- Buena Vista University
- California state University
- Carleton College
- Central Washington University
- Champlain College
- Chicago State University
- Clemson University
- Cleveland State University
- Coastal Carolina University
- College of Santa Fe
- Colorado Mesa University
- Colorado State University
- Columbia University
- Cornell Univeristy
- Covenant College
- Drexel University
- Duke University School of Law
- Duke University, Durham NC
- East Stroudsburg University
- Eastern Illinois University
- Elon University
- Embry Riddle Aeronautical University
- Excelsior College
- Ferris State University
- Florida Agricultural and Mechanical University
- Florida Atlantic University
- Florida International University
- Florida State University
- Fordham University
- Fox Valley Technical College
- Freed-Hardamen University
- Friends University
- George Mason university
- George Washington University
- Georgetown University
- Georgia State
- Griffith University
- Grinnell College
- Grove City College
- Hampshire College
- Hampton University
- Hillsdale College
- Hiram College
- Huntingdon College
- Illinois Institute for Technology
- Indiana University
- Iowa State University
- Jacksonville State University
- Jeff State Community College
- Johns Hopkins Univerisity
- Kalamazoo College
- Kennesaw State University
- Kentucky State University
- Kettering University
- Lebanon Valley College
- Lee University
- LeTourneau University
- Liberty University
- Lincoln University of Pennsylvania
- Marian University
- Mary Baldwin College
- Massachusetts Maritime Academy
- McHenry County College
- Mercer University
- Mercyhurst College
- Meredith College
- Miami University
- Michigan Technological University
- Middle Tennessee State University
- Millersville University
- Montana State University
- Montana Tech
- Naval Post Graduate School
- New York University
- Northeastern University
- Northern Arizona University
- Northern Michigan University
- Northwest Nazarene University
- Northwestern University
- Oberlin College
- Oglethorpe University
- Oklahoma Baptist University
- Old Dominion University
- Olympic College
- Orange Coast College
- Pacific Lutheran University
- Pennsylvania State University
- Pepperdine University
- Pomona College
- Randolph-Macon College
- Regent University
- Regis University
- Rhode Island School of Design
- Robert Morris University
- Rochester Institute of Technology
- Roger Williams University
- Roosevelt University
- Rutgers University
- Saint Anselm College
- Saint Joseph's University
- Salve Regina University
- Shepherd University
- Southern Methodist University
- St. Anselm College
- St. John's College
- State University of New York
- Stevens Institute of Technology
- Swarthmore College
- Texas A&M University
- The Citadel
- The New England Institute of Art
- The University of South Carolina
- Trinity University
- Tulane University
- University of Wisconsin
- University of Auckland, New Zealand
- University of California, Santa Cruz
- University of California, Los Angeles
- University of Central Texas
- University of Colorado
- University of Connecticut
- University of Dallas
- University of Florida
- University of Georgia
- University of Hawai'i-Manoa
- University of Illinois
- University of Michigan
- University of Minnesota
- University of Mississippi
- University of Missouri
- University of Nevada
- University of New Haven
- University of New Haven
- University of North Carolina
- University of Northern Iowa
- University of Oklahoma
- University of Otago
- University of Pennsylvania
- University of Pittsburgh
- University of Southern California
- University of Southern Indiana
- University of Sussex
- University of Tennessee
- University of Texas
- University of Utah
- University of West Alabama
- University of West Georgia
- University of Wisconsin
- University West Florida
- US Air Force Academy
- Utah Valley University
- Villanova University
- Virginia Military Institute
- Virginia Tech
- Washington State University
- Webster University
- West Chester University
- West Virginia University
- West Virginia Wesleyan College
- Western Kentucky University
- Western Michigan University
- Wheaton College
- Wheaton College (IL)
- William and Mary
- William Jewell College
- Wright State University
- Yale University
- Yonsei University
CALCULUS I: ACADEMICS
Through the usage of a computer algebra system like LiveMath™ - you will never miss a minus sign again!
Although the driving of a computer algebra system requires some up-front time to learn and master, once completed (rather quickly for most students), the time saved from having to be a "minus sign accountant" adds to the productivity of your study time. If you have ever spent hours looking for that "little numerical error", you know what we mean.
Command of a computer algebra software system is a modern-day necessity of mathematical academics. It is important, however, to retain a meaningful command of paper/pen/pencil manual computations as well. Our blend of curriculum strives for an 80%/20% split between computer algebra usage and manual computation and written skills. With each module in our curriculum, a concluding Literacy Sheet assignment ensures that each student has written mathematical competency in the subject area.
The proctored final exam is a written exam away from the computer. It is these Literacy Sheet assignments, and the continuing bridge from modern computer algebra software back to classical, manual mathematics that prepares the student from this written final exam.
We do not have any multiple-choice work. We are a real collegiate-level course program - not a "canned" set of multiple-choice question sheets which are common from large publishers and degree-mill schools.
Calculus I Example Course Materials
Videotext - A Modern Replacement of the Textbook
What is a videotext? It is like a textbook, except instead of being based upon printed information, this "text" is based upon video presentations as the core method of explaining the course topics. Instead of a huge, thick 1000-page Calculus textbook to lug around in your backpack; course materials are a combination of computer algebra notebooks, video presentation, screen video presentations, PDF "literacy sheets" to be completed by hand on paper with pen/pencil.Example Videos are in MP4/H.264 format, which play in most modern browsers without additional software.
Our videotext features two main types of videos:
- Screencast Videos using LiveMath™ Play Video
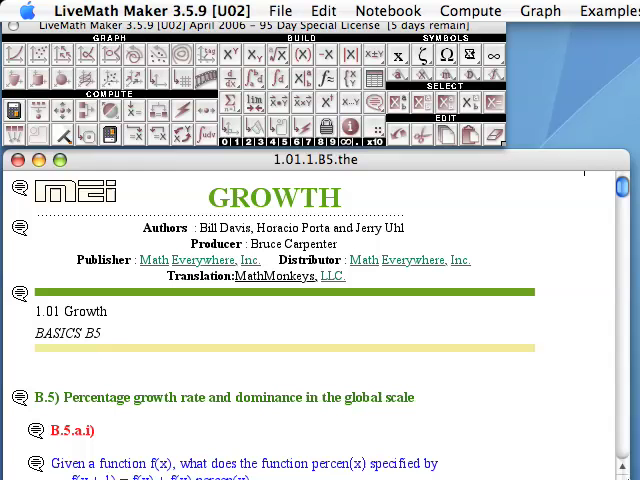
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus 1 at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
- ChalkTalk Videos: Manual Calculations Play Video
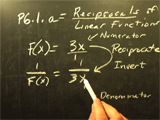
While using a computer algebra software package is a very cool way to do Calculus computations and investigations, we must also pay attention to the classical side of Calculus, and the computations that can be completed by hand with paper/pen/pencil. To be a well-rounded Calculus student, you need to be able to do calculations in both technical and manual methods.
Calculus I Screencast Video Questions
One extremely powerful aspect of the Distance Calculus course technologies is the usage of screencast video (and audio) recordings made by the students and the instructors, exchanged just as easily as emails back and forth.
If a picture is worth a thousand words, then a screencast movie is worth a million words - and saves boatloads of time and effort.
Instead of trying to type out a math question about a particular topic or homework question, the ease of "turning on the screen recorder" and talking and showing your question - in the span of a few minutes - can save hours of time trying to convert your question into a typed (and coherent) narrative question.
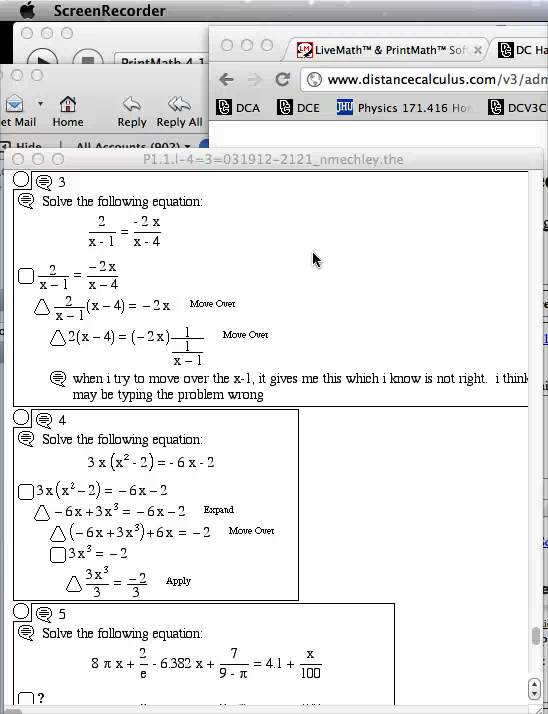
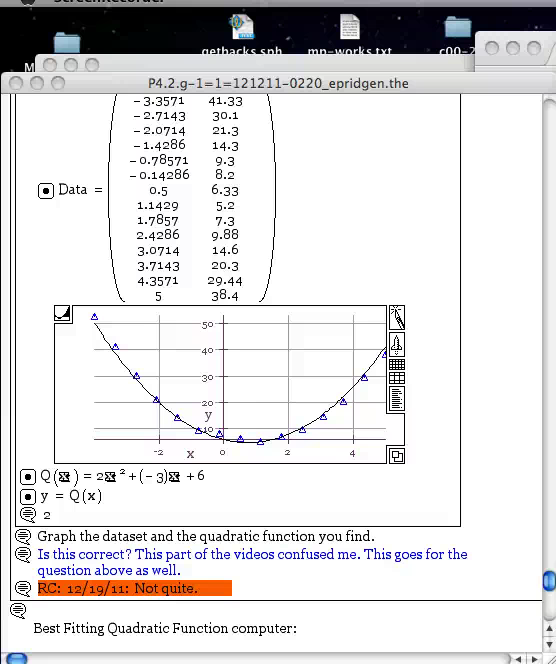
Example Instructor Question/Answer Movie
When a student asks a question in a homework notebook, sometimes the best way to explain the answer is via a screen movie.
- Instructor Question/Answer Movie Play Video
- Instructor Question/Answer Movie Play Video
- Instructor Question/Answer Movie Play Video
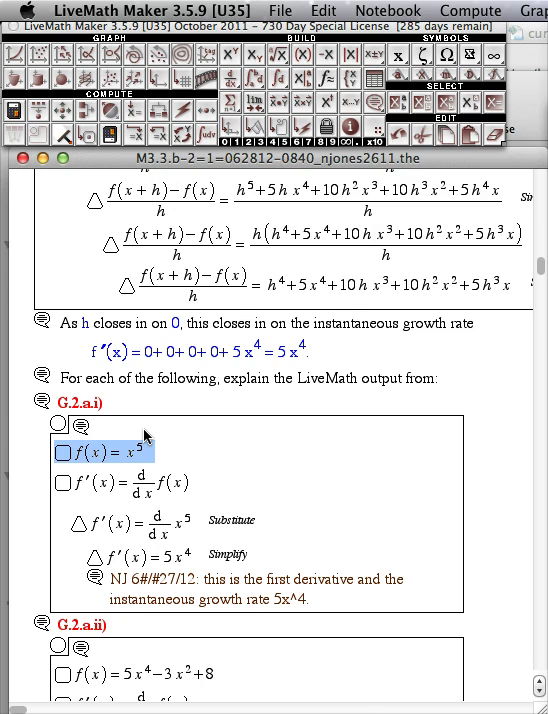
- Instructor Question/Answer Movie Play Video

Calculus I Example Student Work and Grading
The majority of the course work occurs via the exchange of LiveMath™ notebooks - think Word Processing Files, but for mathematical computations instead of just text. The course materials are a combination of those notebooks, along with video resources (screen video recordings and chalkboard presentations).
The student will "Hand-In" a notebook, and one of the instructors will grade, correct, give feedback, and/or give hints on the work in the notebook, and return the notebook to the student in his/her "GetBack" folder, where the student will view the instructor comments.
Sometimes the notebook is deemed "Complete" on the first revision. Sometimes the notebook must go back and forth between the student and instructor a number of times - 2, 3, 4, 5 times is rather common.
Coupled with the screencast video mechanism, sometimes the instructor or the student will submit a screen movie with the notebook, giving further explanation or questions in audio/video format.
Below are some example notebooks from actual students, showing the progression from starting notebook to completed notebook.
- LiveMath™ Course Materials #1 PDF Printout
Course Materials PDF #1
Course Materials PDF #2
Course Materials PDF #3
- LiveMath™ Course Materials Notebook #2 PDF Printout View PDF

- LiveMath™ Course Materials Notebook #3 PDF Printout View PDF

- LiveMath™ Course Materials Notebook #4 PDF Printout View PDF

- LiveMath™ Course Materials Notebook #5: Mean Value Theorem Mean Value Theorem

Distance Calculus - Student Reviews





Date Posted: Aug 16, 2020
Review by: Jennifer S.
Courses Completed: Calculus I
Review: The course was intense and required a lot of hard work. Professors ready available to assist when needed. Professors presented and explained materials/course work in detail and provided explanations and resources.
Transferred Credits to: University of New Haven, West Haven, CT





Date Posted: May 3, 2018
Review by: James Holland
Courses Completed: Calculus I, Calculus II
Review: I needed to finish the Business Calculus course very very very fast before my MBA degree at Wharton started. With the AWESOME help of Diane, I finished the course in about 3 weeks, allowing me to start Wharton on time. Thanks Diane!
Transferred Credits to: Wharton School of Business, University of Pennsylvania





Date Posted: May 3, 2018
Review by: James Holland
Courses Completed: Calculus I, Calculus II
Review: I needed to finish the Business Calculus course very very very fast before my MBA degree at Wharton started. With the AWESOME help of Diane, I finished the course in about 3 weeks, allowing me to start Wharton on time. Thanks Diane!
Transferred Credits to: Wharton School of Business, University of Pennsylvania
Frequently Asked Questions
Yes. Calculus 1 (Calculus I) is intended for science, engineeering, and mathematics students (STEM), whereas Applied Calculus is intended for biology, business, MBA, and other majors and programs where only a single course of Calculus is required. Calculus I uses trigonometric functions, whereas Applied Calculus does not.
Yes. Calculus I is equivalent to the AP Calculus AB course and credit-by-examination system.
No. AP Calculus BC is equivalent to the Calculus II (Calculus 2) course.
Yes. Calculus I uses all of the tools of Precalculus including Trigonometry. Our Calculus I course has a very thorough Precalculus Refresher beginning module for those who have been away from Precalculus for a while.
Yes, All Distance Calculus courses are offered through Roger Williams University in Providence, Rhode Island, USA, which is regionally accredited (the highest accreditation) through New England Commission of Higher Education (NECHE).
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]

