Multivariable Calculus Online Course for Academic Credit
Multivariable Calculus is the sophomore-level Calculus course completed after the
freshman Calculus I-II calculus courses. Multivariable Calculus investigates the calculus
of functions of 2 (or more) input variables, which leads to graphs in 3D for 2 input variables,
and higher dimensions which we cannot graph so easily, but we can still study and analyze by learning
and developing the mechanisms in the 3D case.
| Course Title: | Multivariable Calculus and Vector Analysis |
| Catalog Number: | DMAT 355 |
| Credits: | 4 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for Multivariable Calculus and Vector Analysis |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 355 - Multivariable Calculus and Vector Analysis | |
Our Multivariable Calculus course via Distance Calculus @ Roger Williams University is a beautiful course, full of graphical, numerical, and symbolic investigations using the LiveMath computer algebra and graphing system.
Below you will be able to read more about our Multivariable Calculus course, and watch a few videos explaining some aspects of the course and the curriculum.
Completion of DMAT 355 - Multivariable Calculus earns 4 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
Other Names for Our Multivariable Calculus - DMAT 355
"Multivariable Calculus" has many different names at various other academic institutions. Our "Multivariable Calculus" course is often called these other calculus course names:- Vector Calculus
- Calculus III
- Calculus of Several Variables
- Calculus IV
- Calculus 3
- Calculus 4
"Calculus III" is sometimes a course after Calculus II that has power series, Taylor's Theorem, and some 3D Calculus, perhaps stopping at partial derivatives. Our course is the fuller Vector Calculus course, culminating with the theorems of Green, Gauss, Stokes, and the Divergence Theorem. Sometimes this level of Vector Calculus or Multivariable Calculus is referred to as the "higher Multivariable Calculus course".
Our Multivariable Calculus course is not "Advanced Calculus", which is usually an upper division course for math majors, using texts like Rudin or Apostol, which are courses beginning a study of real analysis, focusing on rigorous mathematical proofs of concepts of calculus.
Multivariable Calculus Online Course for Credit Introductory Videos
Multivariable Calculus Online Course for Credit Introduction
Aften enduring the first-year Calculus I and Calculus II courses on single-variable differentiation and integration theory, undergraduates earn admission to the course where Calculus actually gets fun: 3D Calculus - the Calculus of many variables.Seems easy, right? Instead of functions of one variable - f(x) - we now study functions of two variables:
How does this change to 2 input variables x,y change the theorems of Calculus? What does the Fundamental Theorem of Calculus look like for f(x,y)? What does it mean to take "the derivative" of f(x,y)? What does it mean to take "the integral" of f(x,y)?
In Multivariable Calculus, the graphics from the computer algebra software really come alive.
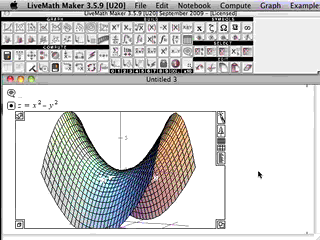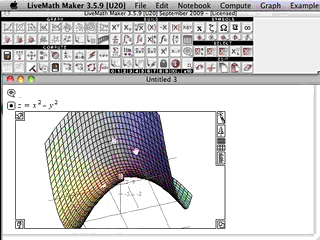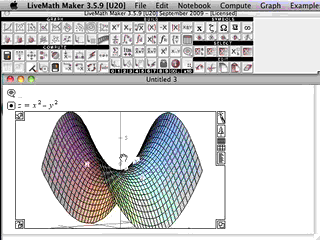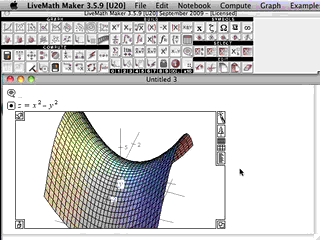
In 2D Calculus, the graphs are rather pedestrian, not much above those graphs you can generated on a graphing calculator. In 3D Calculus, the computer graphics become an indispensible part of the investigation - as essential as needing a microscope to do Biology, or beakers and solutions to do Chemistry.
Our Multivariable Calculus Online course has the following main components:
- Getting Started in LiveMath
A very short mini-course on getting up to speed using our computer algebra and graphing software, LiveMath. 10 short assignments. - Vectors
2D and 3D vectors, graphing them, adding/subtracting, dot and cross products, planes in 3D, getting ready for Vector Fields - Differentiation in 2 or more variables
The generalization of the derivative f'(x) is the gradient vector field ∇f(x,y). In 2D Calculus, the derivative function f'(x) is graphed along with the original function f(x), and the derivative f'(x) is used to measure change (and critical change points) on the function f(x). In 3D Calculus, the "derivative" of f(x,y) is a vector field made from partial derivatives, and can be visualized as lying in the input 2D x-y-plane. We learn how this gradient vector field is used to analyze the properties of the f(x,y) function. - Integration in 2 or more variables
In 2D Calculus, we take integrals of functions f(x), which give us information about the function with different interpretations (area, physics computations, accumulation). In 3D Calculus, the integral is formulated in various ways. Adding a second input variable turns out to complicate matters considerably, and we have to formulate "what does this mean" to overcome these obsticles. Just like derivatives → partial derivatives, we will explore what is meant by single integral, multiple integral, curve integral, and surface integral. - Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus in 1 variable says basically that if you integrate a derivative, you get back to the original function f(x)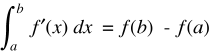
Roger Williams University Course Catalog Listing: DMAT 355 - Multivariable Calculus and Vector Analysis
Course: DMAT 355
Course Title: Multivariable Calculus and Vector Analysis
Transcript Course Title (30 Characters Max:): Multivariable Calculus IV
Course Description: A first course in multivariable differential and integral calculus, with emphasis on computational techniques, vector field analysis, and the generalized Fundamental Theorem of Calculus giving insight to the classical theorems of Green, Gauss, and Stokes. Topics include geometric analysis of multivariable functions, partial derivatives, level curves and surfaces, optimization, properties of vector fields, gradients, potential functions, path integrals and independence, field singularities, divergence and rotation, multiple integration, integral coordinate Jacobian transforms. [4 Semester Credits]
Prerequisite: Successful completion (C- or higher) of Calculus II or equivalent, or consent of instructor.
E-Textbook: Vector Calculus & LiveMath by Robert R. Curtis, Ph.D., adapted from Davis/Porta/Uhl Vector Calculus&Mathematica courseware series
Software: LiveMath
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 355 - Multivariable Calculus and Vector Analysis
DMAT 355 - Multivariable Calculus and Vector Analysis - Learning Outcomes
- 1. To understand the core geometrical elements of Euclidean space
- 2. To understand and compute vector operations and their geometrical interpretations
- 3. To understand and compute partial derivatives and gradient functions
- 4. To understand and compute curves, level curves, surfaces, and level surfaces to multidimensional functions
- 5. To understand and compute vector-valued functions and their geometric representations
- 6. To understand and compute the classical optimization procedure of Lagrange Multipliers
- 7. To understand, compute, and graph vector fields and their associated metrics
- 7. To understand and compute path integrals of vector fields
- 8. To understand, compute, and graph sources, sinks, and singularities of vector fields
- 9. To understand and compute the divergence of a vector field, and its associated computations
- 10. To understand and compute the rotation and curl of a vector field, and its associated computations.
- 11. To understand and compute path integrals in the presence of singularities
- 12. To understand and compute multiple integrals, and their associated geometrical interpretations
- 13. To understand and utilize Fubini's Theorem for reordering integrations
- 14. To understand and compute Jacobian transformations of multiple integrals
- 15. To understand and compute cylindrical, spherical, and other coordinate systems, and their associated measurments with derivatives and integrals
- 16. To understand an introduction to the Generalized Fundamental Theorem of Calculus, and its variations in the Divergence Theorem, and the Theorems of Gauss, Green, and Stokes.
DMAT 355 - Multivariable Calculus and Vector Analysis - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. Vectors 2.1 Geometry of Vectors 2.2 Tangent Vectors; Velocity Vectors, Acceleration Vectors 2.3 Vector Length 2.4 Dot Products 2.5 Vector Projection 2.6 Perpendicularity 2.7 Lines 2.8 Normal Vectors 2.9 Cross Product 2.10 Planes in 3D 2.11 Normal, Binormals, Curvature, Torque 3. The Derivative 3.1 Partial Derivatives 3.2 Gradient 3.3 Level Curves and Surfaces 3.4 Linearization 3.5 Total Differential 3.6 Lagrange Multipliers 4. Vector Fields 4.1 Plotting and Trajectories 4.2 Flow-Along and Flow-Across Curves 4.3 Differential Equations and Vector Fields 4.4 Path Integrals 4.5 Gradient Fields 4.6 Sources, Sinks 4.7 Divergence Theorem 4.8 Singularities 4.9 Rotation and Curl 4.10 Introduction to Potential Functions 5. Multiple Integrals 5.1 Basic Computation 5.2 u-v Transformations; Jacobians 5.3 Measurement of Volume, Mass, Density 5.4 3D Integrals 5.5 Average Value 5.6 Fubini's Theorem 6. Other Coordinate Systems 6.1 Cylindrical Coordinates 6.2 Spherical Coordinates 6.3 Integration in Other Coordinate Systems 7. Gauss, Green, Stokes Theorems 7.1 Green's Theorem 7.2 Stokes' Theorem 7.3 Divergence Theorem 7.4 Generalized Fundamental Theorem of Calculus 7.5 Sources, Sinks, and 3D Gauss's Formula 7.6 Surface Integrals
Legacy Course Connection
Legacy Distance Calculus Course:
DMAT 351 - Calculus of Several Variables
In 2023, Distance Calculus introduced a new catalog of courses. The connection between the old courses and the new courses are given here:
Legacy Course Description: Introduces functions of several variables including partial differentiation; multiple integrals, line and surface integrals, and the theorems of Green, Gauss, and Stokes. (4 credits)
Multivariable Calculus vs. Calculus III
Multivariable Calculus is a course known by many different names at various Colleges/Universities, including:- Calculus III
The third semester of a 4-credit hour Calculus sequence, as it is in our Distance Calculus calculus courses program. - Calculus IV
Usually the fourth quarter of a 3-credit hour Calculus sequence. - Vector Calculus
An appropriate title in that we study vector fields and the generalization of the derivative; most textbooks for this course entitled this way, too. - Multivariable Calculus
The most descriptive moniker, encompassing all aspects of Calculus of more than 1 variable.
At some schools, the Multivariable Calculus curriculum is called "Calculus III", or even "Calculus IV", with the intention of the higher multivariable calculus topics of vector fields, partial derivatives, multiple integrals, gradients, the path and surface integral, and the Gauss/Stokes/Divergence Theorems.
One common way to identify the Vector Calculus / Multivariable Calculus course is how this higher courses basically starts with partial derivatives, then goes through path integration of vector fields in 2D and 3D, multiple integrals, and then the named theorems of Green, Gauss, and Stokes. These core topics will help identify Multivariable Calculus in the list of other calculus courses at other institutions.
| 4-credit Semester | 3-credit Semester/Quarters | |
|---|---|---|
| Calculus I Differentiation + Beginning Integration | Calculus I Differentiation | |
| Calculus II Integration Techniques | ||
| Calculus II Integration Techniques + Sequences/Series/Taylor's Theorem | ||
| Calculus III Sequences, Series, Taylor's Theorem | ||
| Multivariable Calculus Vectors, Gradients/Partial Derivatives, Path Integrals, Green's Theorem, Stokes' Theorem, Divergence Theorem | ||
Excellent Re-Entry Point to Calculus
When non-traditional, older students are returing to academics, after a break that can span years or even decades, a most common question is: Where should I re-enter in the Calculus sequence?If you have completed the Calculus I and Calculus II courses previously (even decades ago), and the concepts of differentiation and integration are remembered at a modest level, then an excellent course to return to the Calculus sequence is via the Multivariable Calculus course.
For the student, Multivariable Calculus is where you usually learn - really learn - the topics from Calculus I and II - not because Multivariable Calculus is harder, but just that you revisit the topics from Calculus I and II, but now looking for how these concepts will generalize from a single variable to multiple variables. It is through this generalization process that many students have the "ah-ha!" moment with the original topics from single variable calculus.
In case you did complete Calculus I and Calculus II previously, but you do not remember the basics of differentiation and integration, then returning to Calculus I or Calculus II is the best plan for success in Multivariable Calculus.
Example Multivariable Calculus Student Profiles
Case 1: Calculus I Done, Calculus II Done; Marching Forward in Multivariable Calculus
Phew! Getting through Calculus I and Calculus II is an achievement!
But if you are a science major, most likely Multivariable Calculus is next on your to-do list.
One indicator of how fast a student can complete Multivariable is the grade earned in Calculus II.
| Typical Completion Timelines for DMAT 355 - Multivariable Calculus | ||||
| Hours Dedicated | Calculus II Grade | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-10 hours/week | C,D | 1-2 hours/day | 16 weeks | Reasonable |
| 7-12 hours/week | C,D | 2-3 hours/day | 14 weeks | Reasonable |
| 10-15 hours/week | C+,B,B+ | 3-4 hours/day | 10 weeks | Reasonable |
| 15-20 hours/week | B | 5-6 hours/day | 8 weeks | Stretched |
| 20-25 hours/week | A | 5-7 hours/day | 6 weeks | Stretched |
| 25-35 hours/week | A+ | 6-8 hours/day | 4 weeks | World's Record |
Time commitments are important for success in an online Multivariable Calculus course for college credit from Distance Calculus. There are no fixed due dates in the Distance Calculus online courses, so it is important that students instead set their schedules for a dedicated amount of time towards the coursework.
It is also very important to consider that going faster through a course is DIRECTLY DEPENDENT upon your math skill level, and your successful engagement of the course. We require that you complete the course in a Mastery Learning format. If you are struggling with the course content, or trying to go too fast where the quality of your submitted work is suffering, then the instructors will force a slow-down of your progress through the course, even if you have fixed deadlines.
Case 2: Undergraduate Science Major
Marco is a undergraduate engineering major, and part of his degree program dictates that he finish Multivariable Calculus. Marco did pretty well in Calculus I and Calculus II. Rather than more lectures/taking notes/Problems 1-99 odd, Marco wants to change things up, and to take the Multivariable Calculus course via the Distance Calculus calculus courses.How fast can Marco complete the Multivariable Calculus online course?
The answer to this question depends mostly on when Marco plans to work on the course.
The most successful time for Marco would be during winter, spring, or summer breaks from his regular course load. By modifying his schedule to work on the Multivariable course during these "off times", Marco will be able to concentrate and focus just on the Multivariable Calculus course, and his tendency towards success will increase dramatically.
If Marco must complete the Multivariable Calculus course during the regular semester, as part of the other 3-5 courses he is taking, trying to fit Multivariable Calculus in there will be challenging (although not as challenging as trying to do the same for Calculus II, as it turns out). Here are some timelines for such a plan:
| Multivariable Calculus Online Course Plan With Full Course Load Otherwise | ||||
| Hours Dedicated | Calculus II Grade | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 9 hours/week | C | 3 hours/day, 3 days/week | 18 weeks | Reasonable |
| 12 hours/week | C | 3 hours/day, 4 days/week | 14 weeks | Reasonable |
| 12 hours/week | B | 3 hours/day, 4 days/week | 12 weeks | Reasonable |
| 15 hours/week | B | 3 hours/day, 5 days/week | 10 weeks | Stretched |
| 15 hours/week | A | 3 hours/day, 5 days/week | 8 weeks | Stretched |
| 18 hours/week | A+ | 3 hours/day, 6 days/week | 6 weeks | Ambitious |
Case 3: Returning To Graduate School: Rushed
Karen just got accepted into Graduate School in Economics towards a Ph.D. She has a conditional acceptance, and must finish Multivariable Calculus in a very short time. Karen also works full time.What must Karen do to finish Multivariable Calculus Online Course?
The "short time" needs to be on the order of 3-4 weeks for Multivariable Calculus. Anything less is quite impossible. While Multivariable Calculus is a bit easier than Calculus II, the Multivariable Calculus course still has its challenges, and time-on-task will still require a significant time committment with enough rest spots for the concepts to "sink into the brain sponge".
Karen will need to plan for large blocks of time to dedicate towards the course. If shooting for 4 weeks completion, then at least 8-10 hours per day. If shooting for 6 weeks completion, then 6-8 hours per day, every day. It will be a very challenging 4-6 weeks.
Karen should also be ready that the course takes a little longer than the planned 4-5 weeks. Going a week or two over to 6-8 weeks is quite common. Usually graduate schools are quite understanding of the situation of "I'm almost done", and in many cases, the graduate school will give a short extension to aid the student with harsh deadlines.
Karen must understand that even though there are some tough deadlines with this plan, that does not mean that "corners are cut" in the Multivariable course because of these extenuating circumstances. There is only 1 way through the course, and that is the right way.
Case 4: Returning To Graduate School: Methodical
Thomas is applying to Graduate School in Biostatistics towards a Ph.D., and will start in 1 year. Thomas knows she must complete Multivariable Calculus prior to starting that course work (and even before submitting the graduate school application).What will the Multivariable Calculus online course look like for Thomas?
Thomas is not in a rush, yet he wants to finish the course methodically, in a timely manner, as quickly as possible. As Thomas is a Ph.D. bound student, he is highly motivation and task-completion oriented. Some timelines for Thomas for Multivariable Calculus might look like this:
| Graduate-Bound Student Timelines for DMAT 355 - Multivariable Calculus | ||||
| Hours Dedicated | Calculus II Grade | Dedication | Completion Time | Advisory |
|---|---|---|---|---|
| 5-7 hours/week | C | 1-2 hours/day | 18 weeks | Relaxed |
| 8-12 hours/week | B | 2-3 hours/day | 10 weeks | Reasonable |
| 10-14 hours/week | B+/A | 3-4 hours/day | 8 weeks | Reasonable |
| 14-20 hours/week | A | 4-5 hours/day | 6 weeks | Ambitious |
Case 5: Lack of Success in Classroom Multivariable Calculus Course
Mike took Calculus I and Calculus II and did OK in the courses, earning C grades. Then Mike went onto Multivariable Calculus, hoping to improve his grades above the C level. One thing led to another, and Mike didn't succeed in the traditional, classroom Multivariable Calculus course.Mike loathes the thought of returning to the classroom lecture for Multivariable. The lectures were not that much fun going through them the first time, and trying to sit through them a second time will be more than just painful.
Mike wants to change gears, and try something new - taking Multivariable Calculus online course via the Distance Calculus calculus courses.
Typically, students like Mike will take the course over the summer months, and be able to focus just on the Multivariable Calculus course, without being overwhelmed by multiple courses all vying for Mike's attention.
Mike should plan to take a step back, a deep breath, and engage the online course as if starting on a marathon race. Just because Mike "had Multivariable Calculus already", this poor foundational knowledge will not help Mike succeed in this second (and quite different attempt).
Mike would be approaching Multivariable Calculus from a completely different viewpoint than his previous attempt, which certainly goes a long way to minimizing the "review" nature of repeating a course. When going through the new Multivariable Calculus course, all will see things he saw before (e.g. partial derivatives, path integrals, etc.), but completely different types of questions that he probably saw in the classroom/textbook course. An open mind, and genuine academic curiousity to investigate and embrace the new style of work will be required for success.
Mike should plan for a minimum of 12 weeks to engage the online course, even during the summer. It will take time for the course concepts and materials to "sink in" and become comfortable.
We have had many students like Mike succeed in Multivariable Calculus where their classroom experience with Multivariable Calculus was a failure. However, we have also had many students like Mike who discover that the reason they didn't succeed in their first attempt at Multivariable Calculus was an indicator that their math skills are not strong, their interest in math is weaker, and their chosen course study plan may need to change upon failure in two different course paradigms.
Case 6: Life After AP Calculus BC Exam
Rebecca is a hot-shot high school student. She has completed AP Calculus BC exam (equivalent to Calculus II), and now she is ready for the next course. Few (if any) high schools offer the course after AP Calculus BC, which is the Multivariable Calculus course.Rebecca will most likely be able to finish the Multivariable Calculus online course very quickly with a dedicated effort that is quite natural for her. 6-8 weeks is the common time frame.
However, Rebecca may discover that Multivariable Calculus via Distance Calculus is an adult course, and quite unlike the high school course paradigm that he has been so successful in previous. Some students like Rebecca can find Multivariable Calculus more difficult than they anticipated, and they have to dedicate more time and effort than they had planned to budget for.
While Rebecca can earn collegiate credits for Multivariable Calculus in a similar way that AP Calculus BC would earn, Rebecca would not benefit from the inflated GPA multiplier that AP courses help with high school GPAs.
Referenced Colleges/Universities From Our Multivariable Calculus Students
Over the past 27 years, Distance Calculus have enrolled thousands of students who successfully complete our online calculus courses, and use this Official Academic Transcript record towards undergraduate and graduate programs at various colleges and universities in the U.S. and throughout the world.
Below is a list of schools that Distance Calculus - Multivariable Calculus students have listed as their Home Institution:
- Armstrong Atlantic State Univeristy
- Belmont University
- Bloomsburg University
- Boston University
- Clemson University
- Cornell University
- California State University, Dominguez Hills
- Denison University
- Drexel University
- Florida International University
- Florida State College, Jacksonville
- Fresno State University
- Gannon University
- Georgia Institute of Technology
- Georgia State University
- Governor's State University
- Hillsdale College
- Harvard University, Kennedy School of Government
- La Sierra University
- Liberty University
- Mercer University
- Missouri University of Science and Technology
- Montana State University
- University of Montana
- New Mexico State University
- Northeastern University
- Oregon State University
- Portland State University
- Rowan University
- San Diego State University
- Santa Fe Community College
- South Dakota School of Mines and Technology
- St. Mary's College of Maryland
- Texas A&M
- Texas Tech University
- The Catholic University of America
- The Citadel, Military College of South Carolina
- The College of St. Scholastica
- The Master's College
- The University of Alabama
- TUI University
- Tulane University
- University of Alabama, Huntsville
- Union University
- United States Air Force Academy
- United States Military Academy
- Univeristy of Puget Sound
- University of Central Florida
- University Of Connecticut
- university of illinois
- University of Kentucky
- University of Massachusetts, Amherst
- University of Minnesota
- University of Missouri, Columbia
- University of Montana
- University of New Orleans
- University of North Dakota
- University of Notre Dame
- University of Pennsylvania
- University of Pittsburgh
- University of Portland
- University of Richmond
- University of Southern California
- University of Texas at Austin
- University of Wyoming
- Utah State University
- Villanova University
- Walla Walla University
- Washing State University
- Webster University
- Westminster College
- William Jewell College
- Yale University
Multivariable Calculus: 80% Computer Algebra, 20% Pencil/Paper, 0% Multiple Choice
Through the usage of a computer algebra system like LiveMath™ - you will never miss a minus sign again!
Although the driving of a computer algebra system requires some up-front time to learn and master, once completed (rather quickly for most students), the time saved from having to be a "minus sign accountant" adds to the productivity of your study time. If you have ever spent hours looking for that "little numerical error", you know what we mean.
Command of a computer algebra software system is a modern-day necessity of mathematical academics. It is important, however, to retain a meaningful command of paper/pen/pencil manual computations as well. Our blend of curriculum strives for an 80%/20% split between computer algebra usage and manual computation and written skills. With each module in our curriculum, a concluding Literacy Sheet assignment ensures that each student has written mathematical competency in the subject area.
The proctored final exam is a written exam away from the computer. It is these Literacy Sheet assignments, and the continuing bridge from modern computer algebra software back to classical, manual mathematics that prepares the student from this written final exam.
We do not have any multiple-choice work. We are a real collegiate-level course program - not a "canned" set of multiple-choice question sheets which are common from large publishers and degree-mill schools.
Multivariable Calculus Online Course for Credit Example Curriculum
Videotext - A Modern Replacement of the Textbook
What is a videotext? It is like a textbook, except instead of being based upon printed information, this "text" is based upon video presentations as the core method of explaining the course topics. Instead of a huge, thick 1000-page Calculus textbook to lug around in your backpack, all of this new "videotext" can be loaded into your iPods or iPhones (and soon, the iPad!).
Example Videos are in MP4/H.264 format, which will play in all modern web browsers.
Our videotext features two main types of videos:
- Screencast Videos using LiveMath™ Play Demo
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
- Screencast Videos using LiveMath™ Play Demo
Although we are anywhere from a few miles to a few thousand miles apart, watching these screencast videos is like sitting next to the course instructor, watching his computer, learning the topics of Calculus at the same time as learning how to drive the computer algebra and graphing software LiveMath™. These LiveMath™ screencast videos make up the majority of the video presentations in the videotext.
Multivariable Calculus Screencast Video Questions
One extremely powerful aspect of the Distance Calculus course technologies is the usage of screencast video (and audio) recordings made by the students and the instructors, exchanged just as easily as emails back and forth.
If a picture is worth a thousand words, then a screencast movie is worth a million words - and saves boatloads of time and effort.
Instead of trying to type out a math question about a particular topic or homework question, the ease of "turning on the screen recorder" and talking and showing your question - in the span of a few minutes - can save hours of time trying to convert your question into a typed (and coherent) narrative question.
Example Instructor Question/Answer Movie
When a student asks a question in a homework notebook, sometimes the best way to explain the answer is via a screen movie.
- Instructor Question/Answer Movie Play Video
- Instructor Question/Answer Movie Play Video
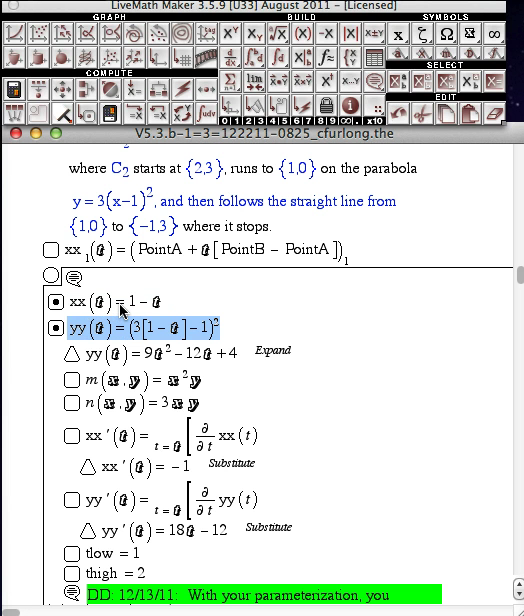
- Instructor Question/Answer Movie Play Video
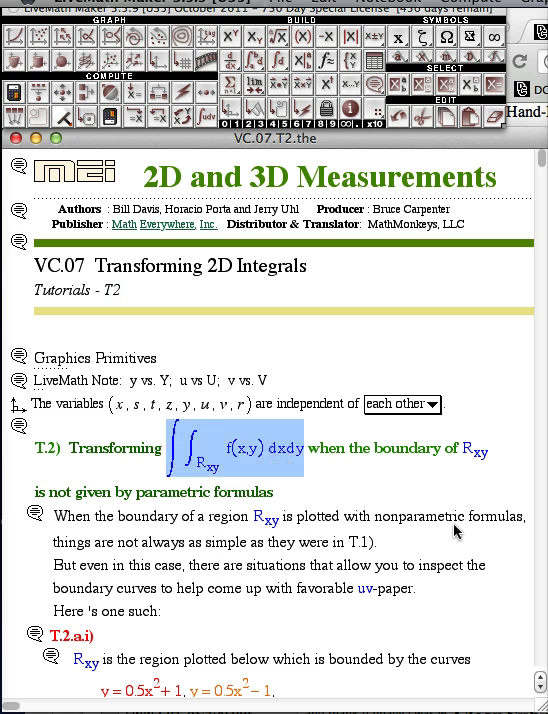
Distance Calculus - Student Reviews




Date Posted: May 21, 2020
Review by: Chester F.
Courses Completed: Calculus I, Calculus II
Review: I did not enjoy Calculus I at my school. I retook Calculus I, and then Calculus II, over the summer via Distance Calculus and it was awesome. I started my sophomore year back on track and ready for my physics classes. I struggled with the MathLive software but I guess it was alright.
Transferred Credits to: University of North Carolina





Date Posted: Apr 29, 2020
Review by: Harlan E.
Courses Completed: Calculus I, Calculus II
Review: I did not do well in AP Calculus during my senior year in high school. Instead of trying to cram for the AP exam, I decided to jump ship and go to Distance Calculus to complete Calculus I. This was awesome! I finished Calculus I in about 6 weeks, and then I kept going into Calculus II. I started as a freshman at UCLA with both Calculus I and II done!
Transferred Credits to: University of California, Los Angeles





Date Posted: Jan 12, 2020
Review by: Mark Neiberg
Courses Completed: Calculus I, Calculus II, Multivariable Calculus
Review: Curriculum was high quality and allowed student to experiment with concepts which resulted in an enjoyable experience. Assignment Feedback was timely and meaningful.
Frequently Asked Questions
Yes, most definitely. Multivariable Calculus is one of the core courses needed for starting any degree program in Data Science. In fact, you need all of the Calculus sequence courses before you start Data Science!
No, Multivariable Calculus studies the generalization of Calculus of a single variable (Calculus I and II) to 2 or more variables. The ideas of the derivative and the integral generalizes in very beautiful ways into higher dimensions.
Sort of. Multivariable Calculus has many other names: Calculus III, Calculus IV, Vector Calculus; each is usually split up with different topics. Our Multivariable Calculus is intended to satify all the equivalent courses; as such, it is a longer course.
99% of the time - yes! But follow the instructions on our Transferring Credits page to make sure you ask AHEAD OF TIME for permission from your college/university to this course.
Yes, All Distance Calculus courses are offered through Roger Williams University in Providence, Rhode Island, USA, which is regionally accredited (the highest accreditation) through New England Commission of Higher Education (NECHE).
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]

